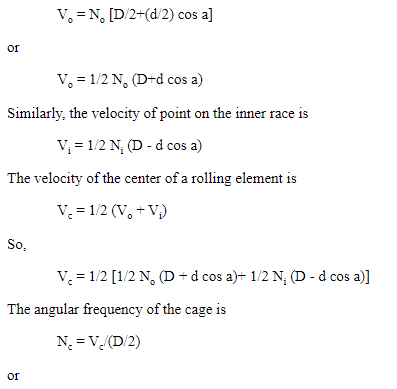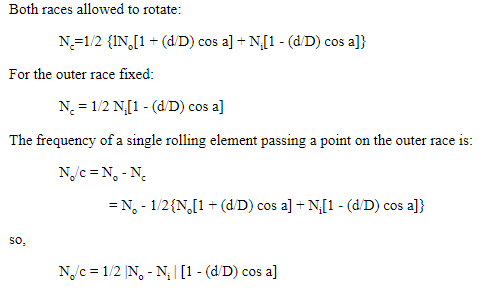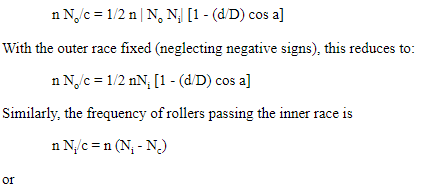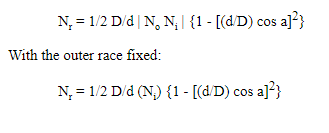The topic is about Rolling Element Bearing Frequencies Derivation of Bearing Frequencies.Primary Rolling Element Bearing Frequencies. Cage Frequency. Race Ball Pass Frequency.
Rolling Element Bearing Frequencies
These calculated frequencies are essentially of academic interest, because (1) it frequently occurs that any flaw on any element rapidly generates secondary flaws on other elements and (2) knowledge of the existence and extent of a flaw is vital; however, the element that it is on is not too important because the entire rolling element bearing is normally replaced and not just the damaged portion.
Rolling element bearings find many uses in today’s machinery. They can be found in motors, slow-speed rollers, gas turbines, pumps, and many other machines. Some of the reasons rolling element bearings are used are: low starting friction, low operating friction, ability to support loads at low (even zero) speed, lower sensitivity to lubrication (compared to fluid film bearings, thus a simpler lubrication system can often be used), and the ability to support both radial and axial loads in the same bearing. When some of these factors are important, rolling element bearings may be in use.
By themselves, rolling element bearings have very little damping, so whenever a machine with rolling element bearings traverses a balance resonance, large vibration can result. Also, compared to fluid film bearings which generally have a long life, rolling element bearings have a limited fatigue life due to the repeated stresses involved in their normal use.
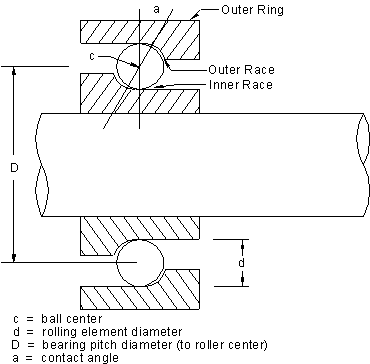
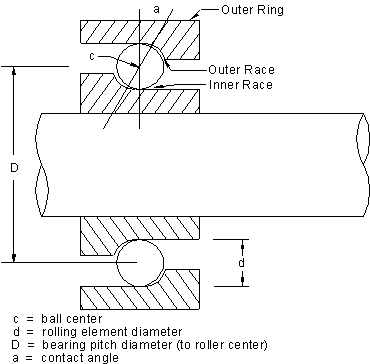
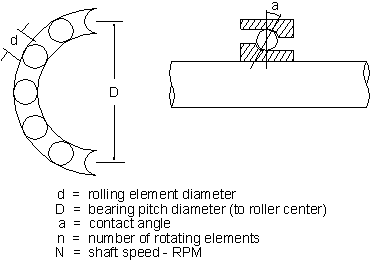
Rolling element bearings, regardless of type (ball, cylindrical, spherical, tapered, or needle) consist of an inner and outer race separated by the rolling elements, which are usually held in a cage (see Figure.
Mechanical flaws may develop on any of these components. Using the basic geometry of a bearing, the fundamental frequencies generated by these flaws can be determined.
For most applications, the outer race is fixed and does not rotate. However, in some instances, just the outer race or both races rotate. For the case of the outer race fixed, Following figure contains a summary of the main bearing frequencies. These frequencies may, and often do, include sum and difference frequencies. Often they are modulated by the speed of the equipment.
Derivation of Bearing Frequencies
The basic geometry for rolling element bearings can be seen in figure 5.
Balls (rolling elements) passing over a flaw on the outer race or the inner race generate the inner and outer roller pass frequencies. These frequencies can be derived from the bearing geometry assuming there is no slippage or dimensional change with load. Rolling element flaws or a defect in the cage can generate the roller spin frequencies; a flaw in a roller can generate a 2X roller spin frequency by hitting both the inner and outer races with each roller rotation. Any of a combination of flaws can generate or be modulated by the cage frequency, the frequency with which the rollers revolve as a set. What follows is a derivation of the primary rolling element bearing frequencies when both races are allowed to rotate and the simplified form when the outer race does not rotate.
Primary Rolling Element Bearing Frequencies
(both races rotating)
Notation as in figure
No = outer race angular speed
Ni = inner race angular speed (= shaft rotative speed)
n = number of rotating elements
a = contact angle
D = bearing pitch diameter
d = rolling element diameter
The following fact is used in the derivation:
- Linear velocity = (angular velocity) x (radius).
Since the outer race radius is [D/2 + (d/2) cos a], the velocity at a point on the outer race is
Cage Frequency
Both races allowed to rotate:
Note: In this equation and all following equations, the mathematical sign stands for the absolute value of the enclosed quantity. The absolute value is always a positive number.
Outer Race Ball Pass Frequency
Both races allowed to rotate:
Inner Race Ball Pass Frequency
Both races allowed to rotate:
Solve for Nr, the roller spin frequency.
Roller Spin Frequency
Both races allowed to rotate:
Summary
The fundamental rolling element bearing frequencies have just been derived with both races allowed to rotate. Figure presents these frequencies with the outer race fixed, not rotating; this is most often the situation. In addition to these calculated rolling element frequencies, the bearing natural frequency can be generated. This frequency can be determined best by testing, not calculation. Knowing these frequencies gives both measurement and diagnostic information. The expected frequency ranges inform us as to the proper measurement system, and they enable us to isolate bearing-related frequencies for diagnostics.
A Practical Example of How to Establish the Required Filter Ranges for a Rolling Element Bearing Application
The following information must accompany any order for rolling element bearing monitors in order to establish the proper filter ranges for the Rotor Vibration and Prime Spike regions:
Bearing manufacturer and manufacturer’s bearing number and type of bearing (e.g., Angular contact ball, Cylindrical roller, etc.)
N = Shaft Speed RPM (or speed range if applicable)
n = Number of Rolling Elements
d = Rolling Element Diameter
D = Bearing Pitch Diameter (roller center to roller center)
a = Contact Angle
A good rule for setting the 1 to 7 times EPx is to use the outer race defect rate to set the 1 EPx and the inner race defect rate to set the 7 EPx cutoff of the filter.
Example:
SKF = N306 Single Row Cylindrical Roller
N = 3600 RPM
n = 11
d = 0.394 Inch
D = 2.007 Inch
a = 0 Degrees
1EPx = (N/2) (n) ((1 (d/D) (cos a))
- = (3600/2) (11) ((1 (.394/2.007) (cos 0))
- = (1800) (11) (0.80)
- = 15,899 RPM
7EPx = (7) (N/2) (n) ((1 + (d/D) (cos a))
- = (7) (3600/2) (11) ((1 + (.394/2.007) (cos 0))
- = (7)(1800) (11) (1.20)
- = 165,810 RPM
Therefore for this particular machine and bearing arrangement, the Rotor Vibration and Prime Spike regions are respectively:
- 1/4 N to 3N = 900 RPM to 10,800 RPM (Rotor Vibration)
- 1EPx to 7EPx = 15,899 to 165,810 RPM (Prime Spike)
Rolling Element Bearing Frequencies Derivation of Bearing Frequencies.Primary Rolling Element Bearing Frequencies. Cage Frequency. Race Ball Pass Frequency.