The quantity of movement equation, also known as the momentum equation, is a fundamental principle in fluid mechanics that describes the conservation of momentum for a fluid flowing through a system. It is derived from Newton’s second law of motion, which states that the rate of change of momentum of an object is equal to the net force acting on it. In fluid mechanics, this principle is applied to fluid elements within a flow field.
What is Momentum Equation?
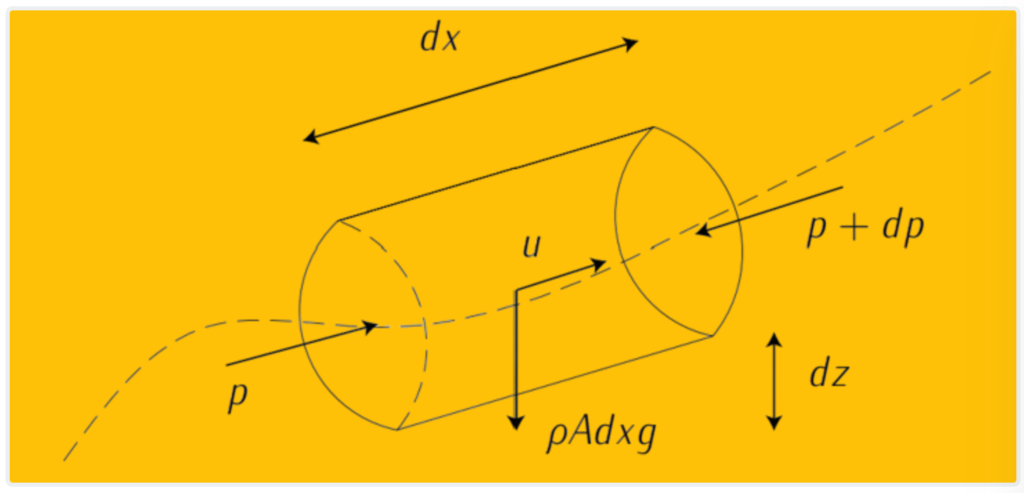
Momentum Equation Formula
The general form of the momentum equation in vector form is:
DV / Dt=F+∂T / ∂V
Where:
- DV / Dt is the material derivative of velocity, representing the rate of change of velocity experienced by a fluid particle as it moves through the flow field.
- F represents the external forces acting on the fluid element, such as gravitational forces or surface forces.
- ∂T / ∂V represents the stress tensor, which accounts for the internal forces within the fluid, including pressure and viscous stresses.
The forces exerted on a fluid can be categorized into two types:
- Distance-exerted forces, such as gravitational, electric, and magnetic forces, which act over a distance and are related to mass or volume.
- Contact-exerted forces, such as pressure or friction forces, which act at the surface of contact between the fluid and its surroundings.
The momentum equation is fundamental in fluid mechanics for analyzing the motion and behavior of fluids in various engineering applications, including aerodynamics, hydrodynamics, and fluid machinery.