The speed of sound, a fundamental property of matter, plays a pivotal role in our understanding of acoustics, fluid dynamics, and the behavior of gases. From the gentle rustling of leaves to the thunderous roar of a jet engine, the speed of sound influences the way we perceive and interact with our environment. In this article, we delve into the fascinating world of sound velocity, exploring its significance, influencing factors, and real-world applications.

What is the Speed of Sound?
The speed of sound, often denoted by v, is the velocity at which sound waves propagate through a medium. It represents the rate at which disturbances in pressure and density travel through a substance, transmitting auditory information from its source to our ears. In a gas, such as air, sound waves consist of compressions and rarefactions, with molecules oscillating back and forth along the direction of wave propagation.
Factors Influencing the Speed of Sound:
Several factors influence the speed of sound in a given medium. One of the primary determinants is the medium’s state variables, namely temperature, pressure, and density. In general, sound travels faster in denser mediums and at higher temperatures. The molecular composition of the medium also plays a crucial role, with gases exhibiting different speeds of sound based on their specific gas constants and adiabatic indices.
Speed of Sound Formula
The speed of sound (v) in a gas can be calculated using the formula:
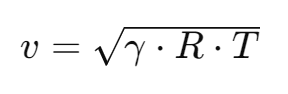
Where:
- γ is the adiabatic index (ratio of specific heats).
- R is the specific gas constant.
- T is the temperature of the gas in Kelvin.
Understanding the speed of sound has numerous practical applications across various fields. In aviation, it is crucial for determining aircraft performance, designing sonic booms, and ensuring efficient communication between air traffic control and pilots. In medicine, it aids in ultrasound imaging, allowing for non-invasive diagnostics and medical procedures. Moreover, industries rely on acoustic principles to optimize the design of musical instruments, speakers, and architectural acoustics for concert halls and auditoriums.
Speed of Sound Basic Understanding
We hear sounds all around us every day, from car horns to music. But have you ever wondered how fast these sounds travel through different things? That’s what we’ll explore.
First, let’s talk about speed. Speed is how fast something moves from one place to another. When it comes to sound, we measure how far it travels in a certain amount of time.
Speed, defined as the ratio of distance traveled (D) to the time taken (t), forms the basis of understanding how quickly sound propagates through a medium. Mathematically, the speed of sound (s) can be expressed as:
s=D / t
Sound is like a wave that moves through stuff, like air or walls. When something makes a sound, it pushes the air molecules together, creating a kind of push-and-pull effect. This is what we hear as sound.
Different things can carry sound waves. For example, air carries sound when someone talks, and walls carry sound when you hear noises from another room. But sound can’t travel through empty space.
The speed of sound depends on a few things. One important factor is how close together the molecules are in the material it’s traveling through. Another is how heavy those molecules are. Temperature and the material’s state (like solid, liquid, or gas) also matter.
In our lab, we’re going to see how different materials affect the speed of sound. By doing experiments, we’ll learn how the properties of a material, like how closely packed its molecules are, impact how fast sound can travel through it. Understanding the speed of sound helps us learn more about how waves move and how materials affect them. It’s an exciting journey of discovery into the world of sound and physics!

Speed of Sound in Air
Let’s break down the procedure for estimating the speed of sound in air using a simple experiment:
Materials Needed:
- Stopwatches
- Metric tape measures
- Trash can lids
- Hammers (or similar noisemakers)
Procedure:
- Measure and Mark Out Distance: Begin by measuring and marking out a distance of at least 200 meters or more in a large field, such as the one in front of Yerkes Observatory.
- Setup Participants: Send one member of your group to the measured distance away with a trash can lid and a hammer. Another member will be in charge of the stopwatch, while a third member will record the data.
- Ready, Set, Bang!: Ensure everyone is in position. The person with the hammer will bang the trash can lid with it.
- Timing the Sound: The member with the stopwatch starts the timer as soon as they see the hammer hit the trash can lid. They stop the timer when they hear the sound. Note that these two events will be close together but not simultaneous, so pay close attention.
- Repeat Measurements: Repeat this measurement at least ten times to get an average of your results.
By following these steps and recording the time it takes for the sound to travel from the point of impact to your ear, you can estimate the speed of sound in air. This simple yet effective experiment offers a direct and intuitive way to understand the fundamental principles of sound propagation.
Speed of Sound from Echoes
Following is the procedure for estimating the speed of sound using echoes:
Materials Needed:
- Yerkes Observatory wall
- 2 wooden blocks (or any objects to create a loud noise)
- Computer with an oscilloscope program and microphone
Procedure:
- Distance Measurement: Stand approximately 50 meters away from the wall and measure your exact distance from the wall.
- Setup: Place the computer and microphone next to you, ensuring they are ready for recording.
- Sound Creation: Clap the two wooden blocks together to create a loud noise. Wait for the echo to bounce off the wall and return to you.
- Recording Time: Using the oscilloscope program, record the time it takes for the sound wave to travel from your clap to the wall and back to you. This time interval will be displayed in the data window of the oscilloscope.
By conducting this experiment and measuring the time it takes for the sound wave to travel to the wall and back, you can estimate the speed of sound. This method utilizes echoes, or reflected sound waves, to determine the velocity of sound propagation. It’s a practical and hands-on way to understand the principles of wave reflection and calculate the speed of sound.
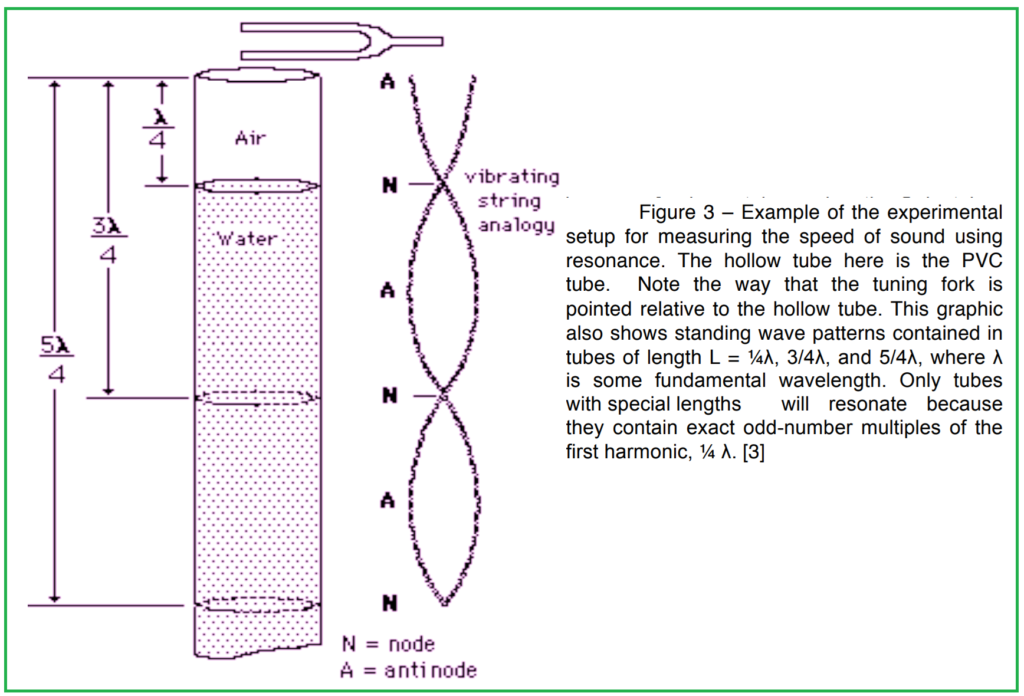
Speed of Sound from Resonance
Here’s a simplified version of the procedure for estimating the speed of sound using resonance:
Materials Needed:
- Water bath (about 1 meter deep)
- PVC tube (length similar to water bath depth)
- Clamp to hold PVC tube submerged
- Tuning fork
- Ruler
Procedure:
- Tuning Fork Frequency: Note the frequency of the tuning fork.
- Setup Table: Create a table in your notebook for recording data.
- Tube Diameter Measurement: Measure the inner diameter of the PVC pipe. Multiply this diameter by 0.4.
- Tube Setup: Submerge the PVC pipe partially in the water bath, leaving only the bottom part submerged.
- Tuning Fork Activation: Strike the tuning fork gently and hold it above the open end of the PVC tube.
- Adjust Tube Length: Slowly raise and lower the tube in the water bath until you hear a significant increase in sound loudness.
- Record Resonance Length: Note the length of tube above the water level when the sound is loudest. Add the correction length from step 3 to this value.
- Identify Additional Resonances: Continue raising the tube to find more resonances, recording each length and adding the correction value.
- Calculate Wavelength: Use the resonance lengths to calculate the wavelength of the sound waves produced by the tuning fork. Wavelength ((\lambda)) is related to resonance length ((L)) by the equation (4L/n = \lambda), where (n) is an odd number (1, 3, 5, etc.).
- Calculate Speed of Sound: Once you have a table of measurements containing the wavelength of the sound produced by the tuning fork, use the wavelength and frequency of the tuning fork to calculate the speed of sound ((v)) using the equation (v = \lambda \times \text{frequency}).
By following these steps and recording the necessary data, you can estimate the speed of sound using resonance. This method utilizes the natural frequencies of the tuning fork and the resonance lengths of the PVC tube to determine how quickly sound waves travel through air.
The Speed of Sound and Density
In this experiment, we’ll explore how different gases affect the speed of sound, building upon our precise measurement of the speed of sound in air using resonance. We’ll replace the air in the PVC tube with various gases of different densities and observe how this affects sound transmission.
We predict that the speed of sound will vary with gas density. As the density of a gas increases, we anticipate that sound will travel more slowly through denser gases compared to air. This expectation is based on the understanding that sound waves propagate through the vibration of gas molecules. In denser gases, molecules are more tightly packed, leading to more frequent collisions and slower transmission of sound waves.
Materials:
- Water bath (approximately 1 meter deep)
- PVC tube (length similar to water bath depth)
- Clamp to hold PVC tube submerged
- Tuning fork
- Ruler
- Pressurized gas cylinders (instructors will handle these)
Procedure:
- Tube Diameter Measurement: Measure the inner diameter of the PVC pipe and multiply it by 0.4 to account for external vibrations.
- Tube Setup: Submerge the PVC tube almost entirely in the water bath.
- Gas Filling: Inform the instructor when ready to fill the PVC tube with a gas other than air. The instructor will slowly fill the tube from a pressurized gas cylinder, ensuring it’s lifted mostly out of the water bath afterward.
- Resonance Detection: Lower the tube slowly into the water, marking each resonance point as you go. Avoid raising the tube out of the water to prevent refilling with air.
- Multiple Measurements: Record all resonance lengths and calculate the wavelength of the tuning fork. If multiple lengths are measured, average them for accuracy.
- Speed of Sound Calculation: Use the tuning fork frequency and calculated wavelength to determine the speed of sound.
- Repeat for Other Gases: Repeat the procedure for each gas available. The densities of these gases are known.
- Data Analysis: Tabulate the results and plot gas density against the speed of sound to observe any relationships.
By conducting this experiment and analyzing the results, we aim to gain insights into how gas density influences the propagation of sound waves. This investigation will contribute to our understanding of acoustic phenomena in different gas environments.

Speed of Sound through Solid Matter
In this part of the experiment, we’ll explore the speed of sound through solid matter, specifically metals. Unlike the previous sections where we focused on gases, sound can travel through any physical medium, including solids. Before we begin the experiment, let’s make some predictions about what we expect to measure for the speed of sound through metals.
Metals are generally much denser than gases. Given their high density, we anticipate that the speed of sound through metals will be faster compared to gases. This prediction is based on the understanding that sound travels more efficiently through denser materials due to the closer proximity of molecules, allowing for faster propagation of sound waves.
Materials Required:
- Laptop computer with sound analysis software (e.g., Macscope)
- Metal pipe
- Microphone connected to the laptop
- Tape
- Hammer
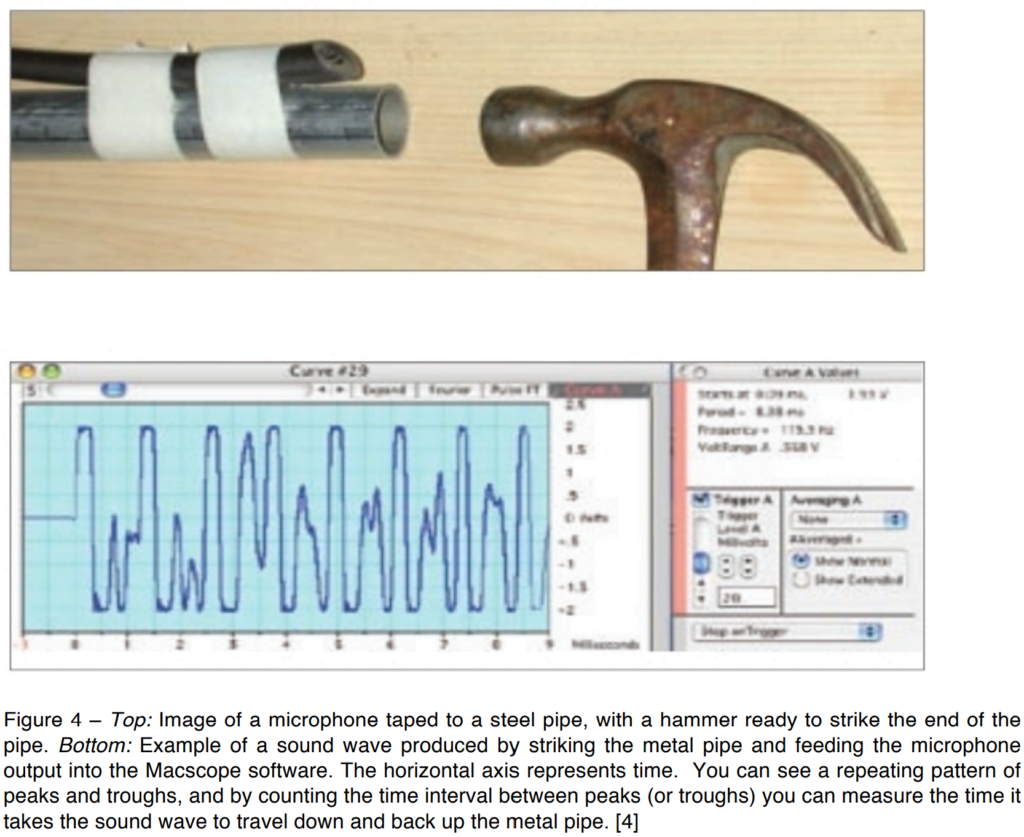
Procedure:
- Experimental Setup: Prepare a metal pipe with a microphone taped to one end and a hammer.
- Software Familiarization: Familiarize yourself with the Macscope software, which displays sound intensity vs. time.
- Trigger Mode Setup: Set the Macscope software to operate in Trigger Mode and adjust the trigger level to ignore background noise.
- Sound Generation: Strike the metal pipe with the hammer and observe the display in the Macscope window.
- Wave Measurement: Count the number of complete waves recorded by Macscope and measure the time taken for the sound wave to create those waves.
- Speed Calculation: Use equation 1 (speed = distance / time) to calculate the speed of sound through the metal pipe. The distance traveled is twice the length of the pipe (down and back up), and the time is the interval measured in step 5.
- Repeat Measurement: If multiple metal pipes are available, repeat the measurement for each metal.
By conducting this experiment, we aim to investigate how the density and properties of metals influence the speed of sound transmission. These findings will contribute to our understanding of acoustic phenomena in solid materials and provide valuable insights into the behavior of sound waves across different mediums.