Mesh Current Analysis is a method used in circuit analysis to find the currents circulating around loops (meshes) in a circuit. It simplifies solving circuits with multiple loops by reducing the number of equations required.
Mesh Current Analysis, also known as Loop Analysis or Maxwell’s Circulating Currents method, is a technique used to simplify the analysis of electrical circuits, especially when dealing with complex networks.
Instead of labeling each branch with a current (Kirchhoff’s Current Law), Mesh Current Analysis labels each “closed loop” in the circuit with a circulating current. This method reduces the amount of math needed and makes solving large circuits more manageable.
Here’s a step-by-step guide to make it easier:
Mesh Current Analysis Steps
- Identify the Meshes: A mesh is a loop that does not enclose any other loops within it. Identify all the meshes in the circuit. In above diagram abcdea is mesh.
- Assign Mesh Currents: Assign a current variable to each mesh. The currents are usually assumed to circulate in a clockwise direction, but you can choose any consistent direction.
- Apply Kirchhoff’s Voltage Law (KVL): Write KVL equations for each mesh. KVL states that the sum of all voltages around a closed loop is zero. Include voltage sources and the voltage drops across resistors (Ohm’s Law: V=IR) in the equations.
- Solve the Equations: Solve the simultaneous equations by cramer’s rule or other to find the values of the mesh currents.
- Determine the Desired Quantities: Use the mesh currents to find the voltages and currents in individual circuit elements, and calculate the power as needed.
Mesh Current Analysis Example 1
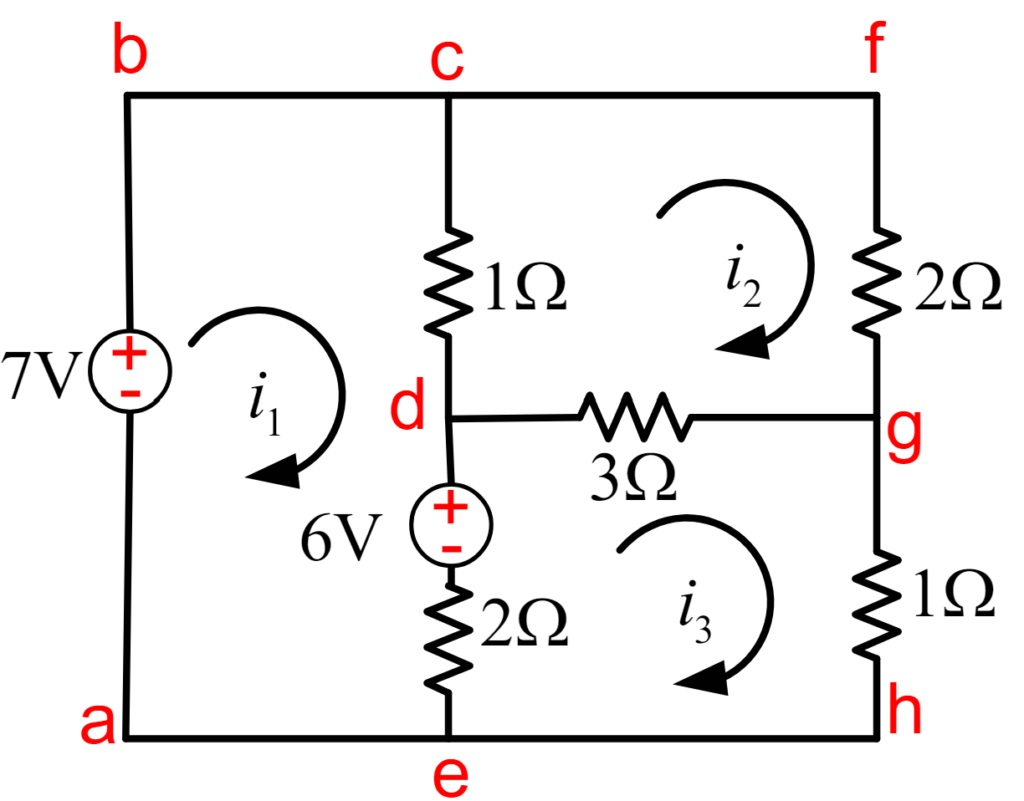
Determine the mesh currents i1, i2, i3 in below circuit diagram.

Step 1: We identified all meshes of circuit as shown in above picture.
Step 2: We assigned all meshes of current which are i1, i2, i3 .
Step 3: Applying Kirchhoff’s Voltage Law (KVL):
so considering the circuit loop abcdea.
1(i1 − i2) + 2(i1 − i3) + 6 − 7 = 0
3i1 − i2 − 2i3 = 1 Equation-1
Now take the 2nd loop cfgdc.
2i2 + 3(i2 − i3) + 1(i2 − i1) = 0
−i1 + 6i2 − 3i3 = 0 Equation-2
Now take 3rd loop dghed.
3(i3 − i2) + 2(i3 − i1) + i3 − 6 = 0
−2i1 − 3i2 + 6i3 = 6 Equation-3
Now take a look on 3 mesh equations 1, 2 and 3.
3i1 − i2 − 2i3 = 1 −i1 + 6i2 − 3i3 = 0 −2i1 − 3i2 + 6i3 = 6
Step 4: Solve the Equations: Here we are using Cramer’s rule to solve the equations.

Mesh Current Analysis involves labeling loops, creating matrices for voltages and resistances, and solving a matrix equation to find the currents. This method simplifies circuit analysis, reducing the amount of math required.