Binary Arithmetic Examples – PLC Professional Course

This article is about Binary Arithmetic Examples. Read Also Previous Articles if you did not read before.

1. Lecture 1: What is Programmable Logic Controller in PLC?
2. Lecture 2: PLC Hardware Components – PC Information
3. Lecture 3: PLC Internal Architecture and Diagram Explanation
4. Lecture 4: What is PLC System? and Working Principle
5. Lecture 5: How to Connect Input Devices to PLC? Input Devices Examples
6. Lecture 6: How to Connect Output Devices to PLC? PLC Output Devices
7. Lecture 7: PLC Applications Examples And Solutions
8. Lecture 8: Numbering System in PLC (Digital System)
9. Lecture 9: The Binary System Concept in PLC
10. Lecture 10: Octal and Hexadecimal Numbering in PLC System
11. Lecture 11: Binary Coded Decimals Examples

Binary Arithmetic Examples

The addition of binary numbers follows the following rules:

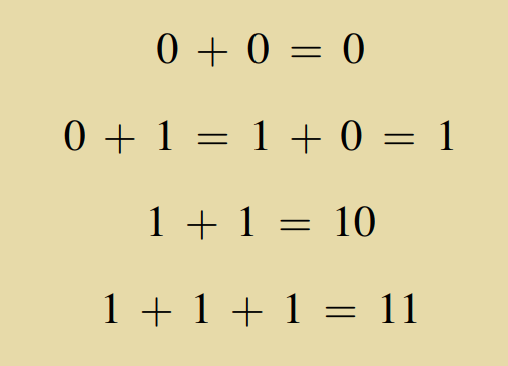
Consider the addition of the binary numbers 01110 and 10011:

   01110
+ 10011
--------
  100001

To perform the addition, we add the corresponding bits from right to left.

For the rightmost bit (bit 0) of the sum, we have 0 + 1 = 1.

Moving to the next bit (bit 1), we have 1 + 1 = 10. We write down the 0 and carry over the 1 to the next column.

For bit 2, we have 1 + 0 + 1 (the carried 1) = 10. Again, we write down the 0 and carry over the 1.

For bit 3, we have 1 + 0 + 1 (the carried 1) = 10. We write down the 0 and carry over the 1.

For bit 4, we have 0 + 1 (the carried 1) = 1.

Thus, the sum of the binary numbers 01110 and 10011 is 100001.

Let’s consider the subtraction of the binary number 10011 from 11011:

   11011
-  10011
--------
   01100

To perform the subtraction, we start from the rightmost bit and work our way to the left.

For the rightmost bit (bit 0), we have 1 – 1 = 0.

Moving to the next bit (bit 1), we have 1 – 1 = 0.

For bit 2, we have 0 – 0 = 0.

Since we need to subtract 1 from 1 in the next column (bit 3), we borrow 1 from the next higher bit. So, we have 10 – 1 = 1.

For bit 4, we have 1 – 0 = 1.

Thus, the difference between the binary numbers 11011 and 10011 is 01100.

Signed Numbers

In binary number representation, numbers are considered unsigned, meaning they have no indication of whether they are negative or positive. However, to handle both positive and negative numbers, a sign bit can be added. In signed numbers, the most significant bit (MSB) is used as the sign bit, where 0 indicates a positive number and 1 indicates a negative number. Thus for an 8-bit number we have:

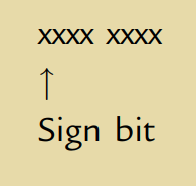
When representing positive numbers in binary, we write them in the usual way with a 0 preceding the binary digits. For example, the positive binary number 10110 is written as 010110.

On the other hand, to represent negative numbers, we use a different notation that provides ease of manipulation for computers. In this notation, negative binary numbers are written by adding a sign bit of 1 before the binary digits. For instance, the negative binary number 10110 is written as 110110.

This alternative representation of negative numbers allows for simpler arithmetic operations and facilitates the implementation of mathematical operations in computer systems.

One’s and Two’s Complements

A more practical way of representing negative numbers is by using the two’s complement method. In this method, a binary number has two complements: the one’s complement and the two’s complement.

The one’s complement of a binary number is obtained by flipping all the bits, changing 1s to 0s and 0s to 1s. For example, if we have the binary number 101101, its one’s complement would be 010010.

The two’s complement is derived from the one’s complement by adding 1 to the least significant bit (LSB) of the one’s complement. Therefore, the two’s complement of 101101 becomes 010011.

The two’s complement representation is widely used in computer systems for performing arithmetic operations and representing negative numbers efficiently.

When representing a negative number using signed two’s complement, we first obtain the two’s complement of the positive number and then sign it with a 1. Let’s consider the representation of the decimal number -6 as a signed two’s complement when using eight bits.

To begin, we write the binary representation for the positive number +6, which is 0000110. Next, we obtain the one’s complement of 0000110, resulting in 1111001. Then, we add 1 to the one’s complement to obtain the two’s complement, which gives us 1111010. Finally, we sign the two’s complement with a 1 to indicate that it is negative.

Therefore, the signed two’s complement representation of -6 in eight bits is 11111010.

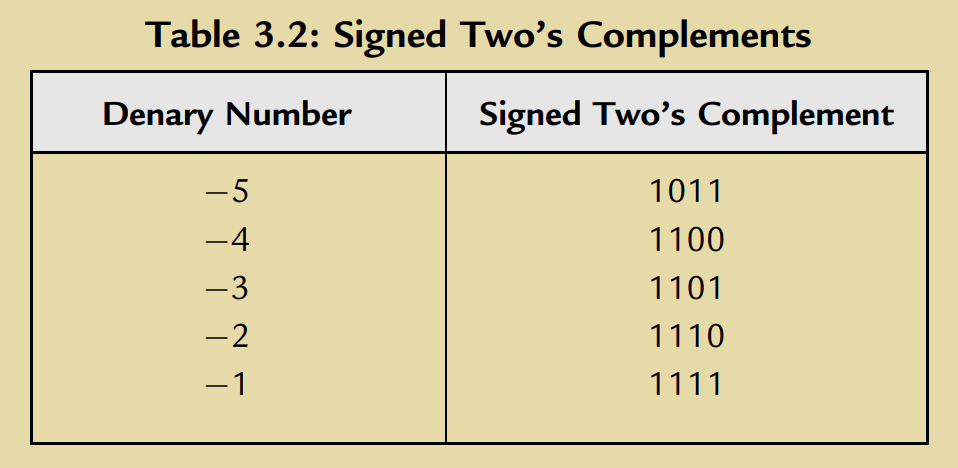
Table 3.2 lists some signed two’s complements for denary numbers, given to 4 bits.

When we have a positive number, we represent it by simply writing the normal binary number with a 0 sign bit. It is only the negative numbers that are written in the two’s complement form.

As a consequence of this representation method, when we add the signed binary equivalents of +4 and -4, which are 0000 0100 and 1111 1100 respectively, we obtain the sum (1)0000 0000. However, within the constraints of the number of bits used, the carry bit represented by the (1) is neglected. Therefore, the result of the addition is simply 0000 0000, which corresponds to zero.

When subtracting a positive number from another positive number, we can consider it as the addition of a negative number to a positive number. In this case, we obtain the signed two’s complement representation of the negative number and then perform the addition with the signed positive number.

For example, to subtract the decimal number 6 from the decimal number 4, we can reframe the problem as (+4) + (-6). We first obtain the signed two’s complement representation of the negative number. Then, we add the signed positive number to this representation.

The most significant bit (MSB) of the resulting number will be 1, indicating a negative value. Therefore, the outcome is a negative number. This represents the 8-bit signed two’s complement representation for the value -2.

When adding two negative numbers, we can obtain the signed two’s complement representation for each number and then perform the addition. It is important to use the signed two’s complement representation for negative numbers and the signed representation for positive numbers.

Floating Point Numbers

Before we delve into floating-point numbers, let’s first discuss fixed-point numbers. Fixed-point numbers are numbers that have a fixed location of the decimal or binary point, which separates the integer part from the fractional part. For instance, 15.3 is an example of a fixed-point decimal number, 1010.1100 is an example of a fixed-point binary number, and DE.2A is an example of a fixed-point hexadecimal number.

When adding two fixed-point binary numbers in an 8-bit system, we consider that the position of the binary point is fixed and the same for both numbers. As a result, we can ignore the binary point during the addition process, perform the addition of the numbers as if they were integers, and then place the binary point back in its fixed position in the result. Let’s illustrate this with an example:

Suppose we want to add 0011.1010 and 0110.1000. we drop the binary point to give:
0011 1010 + 0110 1000 = 1010 0010

Inserting the binary point then gives 1010.0010.

Using fixed-point notation for very large or very small numbers can result in a large number of zeros between the integers and the point, which becomes impractical. To address this, scientific notation is commonly used to represent such numbers. In scientific notation, a number is expressed as a product of a significand (or mantissa) and a power of 10 (or 2 in binary representation).

For example, the number 0.000 000 000 000 023 can be written as 0.23 * 10^-13 or 2.3 * 10^-14 or 23 * 10^-15, depending on the desired precision and representation format.

Similarly, the binary number 0.0000 0111 0010 can be represented in scientific notation as 110010 * 2^-12 (with 12 represented in binary format) or 11001.0 * 2^-11 (with 11 represented in binary format).

This type of notation, where the significand and exponent are separate and can “float” to represent numbers with different magnitudes, is known as floating-point notation. Floating-point representation allows for a wider range of numbers to be expressed accurately and efficiently in computer systems.

A floating-point number is represented in the form of a * r^e, where “a” is referred to as the mantissa, “r” represents the radix or base, and “e” denotes the exponent or power. In the case of binary numbers, the base is understood to be 2, so the representation becomes a * 2^e. When working with binary numbers, there is no need to explicitly store the base since it is already known.

Therefore, a computing system must store not only the sign (positive or negative) but also the mantissa and exponent to represent a floating-point number accurately. By storing these three components, the system can handle a wide range of values, both large and small, with varying degrees of precision.

Floating-point numbers allow for multiple representations of the same value, such as 0.1 * 10^2 and 0.01 * 10^3. To ensure consistency and facilitate arithmetic operations, computing systems normalize these numbers. Normalization involves expressing them in the form of 0.1 * r^e, where “r” represents the radix (base). In the case of binary numbers, this form becomes 0.1 * 2^e.

To account for the sign of a binary number, a sign bit is added. A positive number is represented with a sign bit of 0, while a negative number is represented with a sign bit of 1. For example, the number 0.1001 * 2^–4 becomes 1.1001 * 2^–4 when negative and 0.1001 * 2^–4 when positive.

When performing addition with floating-point numbers, it is necessary to ensure that the exponents are the same. If the exponents differ, a process called exponent alignment or exponent adjustment is performed to make them equal. This adjustment allows for consistent addition and other arithmetic operations on floating-point numbers.