The continuity equation is a fundamental principle in fluid mechanics that describes the conservation of mass for an incompressible fluid flowing through a steady-state, continuous flow. It states that the mass flow rate of fluid entering a control volume must equal the mass flow rate exiting the control volume, assuming there are no sources or sinks of mass within the volume.
Continuity Equation Explanation and its Derivation
Here we will explain about continuity equation and its derivation in context of fluid dynamics, particularly for flowing fluids like air or water, the conservation of mass principle must be interpreted differently from how it applies to closed systems in classical mechanics. Instead of considering individual particles or volumes of fluid, fluid dynamics often employs the concept of a stream tube to understand the continuous flow of mass through a fluid.
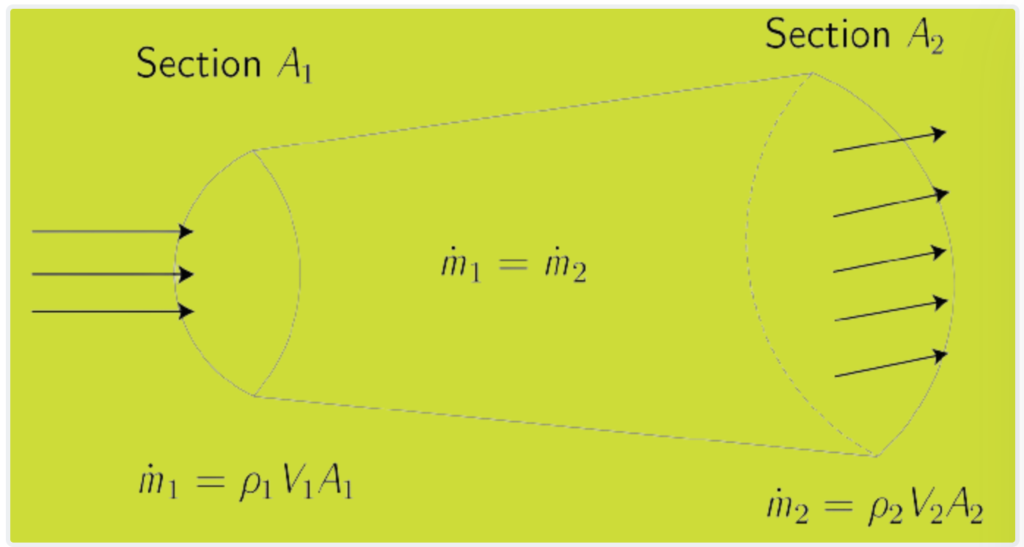
A stream tube is an imaginary pipe-like structure that encompasses a specific volume of fluid within a flow field. It is defined by a set of streamlines that represent the paths followed by individual fluid particles within the tube. Importantly, a stream tube is designed such that there is no flow across its walls, and the flow within the tube is assumed to be steady, meaning that the velocity remains constant across any cross-section of the tube.
With these assumptions in place, the continuity equation for mass flow (( \dot{m} )) through a stream tube states that the product of density (( ρ )), velocity (( V )), and cross-sectional area (( A )) remains constant along the tube:
ρ1V1A1=ρ2V2A2
This equation implies that as the cross-sectional area of the stream tube changes along its length, the velocity of the fluid must adjust accordingly to maintain a constant mass flow rate (( \dot{m} )). In other words, if the cross-sectional area decreases (constriction), the velocity of the fluid must increase to compensate and keep the mass flow rate constant, and vice versa.
Understanding the continuity equation in terms of stream tubes is crucial for analyzing fluid flow in various engineering applications, such as in pipes, channels, or around objects like aircraft or ships. It provides a framework for predicting how fluid properties like velocity and pressure change as the fluid moves through different geometries or conditions.
Compressible and incompressible flow
In fluid dynamics, the difference between compressible and incompressible flow depends on how the density of the fluid changes as it moves.
Incompressible flow:
- In incompressible flow, the density of the fluid remains constant as it moves. This typically occurs in liquids and, under certain conditions, in gases where the flow velocities are relatively low.
- For example, the movement of water through a pipe or the flow of air at speeds below approximately 100 meters per second (m/s) can be considered incompressible.
- In incompressible flow, the density changes in the fluid are negligible, simplifying the analysis of fluid behavior.
Compressible flow:
- In compressible flow, the density of the fluid changes significantly as it moves, often due to variations in pressure and velocity.
- This type of flow is common in gases, especially at high speeds or in conditions where pressure changes are significant.
- For instance, the airflow around a jet airplane traveling at high speeds results in compressible flow.
- Compressible flow is more complex to analyze compared to incompressible flow due to the nonlinear relationship between pressure, density, and velocity changes.
In practical engineering applications, the distinction between compressible and incompressible flow is essential for determining the appropriate models and equations to use when analyzing fluid behavior. While incompressible flow is often simpler to analyze and model, compressible flow must be treated using specialized equations that account for changes in density and pressure.