What is International Standard Atmosphere (ISA)?

The International Standard Atmosphere (ISA) is a way to describe how different factors like pressure, temperature, density, and thickness of the Earth’s air change as you go up in the sky. It’s like a standard reference guide for understanding what the atmosphere is like at different heights. This model helps people in aviation and weather studies have a common understanding of what to expect in the atmosphere, especially when they’re planning things like flights or studying weather patterns.

In simpler terms, think of the ISA as a blueprint that tells us how the air changes as we climb higher into the sky. It helps pilots, engineers, and meteorologists understand what the air is like at different heights, which is really important for things like flying planes safely or predicting the weather. The ISA gives us a standard way to talk about the atmosphere, making it easier for everyone to understand and work with.

Hypotheses for International Standard Atmosphere

Hypothesis 2.1 of the international standard atmosphere, as outlined, specifies several fundamental assumptions that serve as the basis for the International Standard Atmosphere (ISA). Here’s a breakdown of each hypothesis:

The international standard atmosphere adheres to the perfect gas equation, which relates pressure (p), density (ρ), and temperature (T) of a gas. The equation p=ρRT represents this relationship, where R is the specific gas constant for air.

In the troposphere, the lowermost layer of the Earth’s atmosphere, the temperature decreases linearly with altitude. The temperature gradient is constant and defined by the equation T=T0​−αh, where T0​ is the temperature at sea level, α is the lapse rate, and ℎ is the altitude.

Above the troposphere, in the tropopause and lower stratosphere, the temperature remains constant. This is represented by the equation T=T11​, where T11​ is the temperature at the tropopause.

At sea level (altitude ℎ=0), the international standard atmosphere assumes a specific air pressure (p_o​=101325 Pa) and density (p_o​=1.225 kg/m³). These values provide a baseline for atmospheric conditions.

The international standard atmosphere assumes a constant acceleration due to gravity (g=9.80665 m/s²) throughout the atmosphere. This simplifies calculations related to atmospheric dynamics.

The international standard atmosphere assumes that the atmosphere is in a state of calm with respect to the Earth. This means that there are no significant horizontal winds or vertical updrafts or downdrafts.

Fluid Static Equation

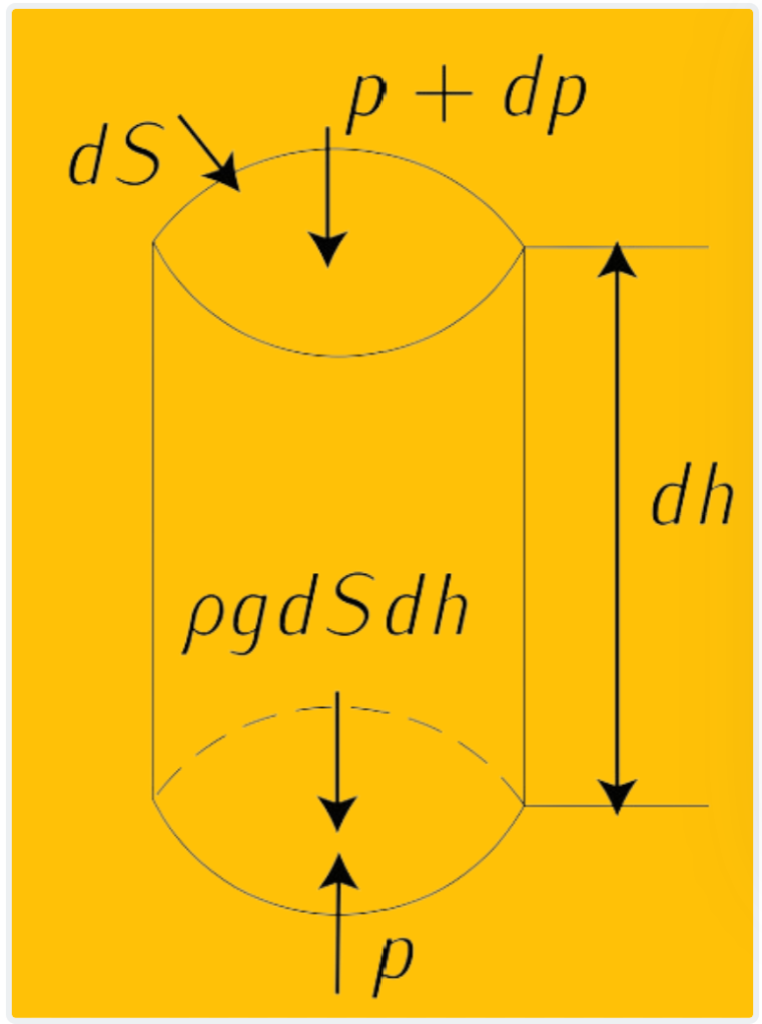
The fluid-static equation, a fundamental principle in fluid mechanics, describes the equilibrium of fluids at rest, particularly in the context of hydrostatics. Hydrostatics is a branch of fluid mechanics that deals with fluids at rest or in a state of constant motion.

When considering air at rest, as outlined in Hypothesis (2.1) of the international standard atmosphere, we can analyze the equilibrium of a differential cylindrical element within the fluid. In this scenario, only two types of forces are at play: gravitational volume forces and pressure surface forces.

The equilibrium of this differential element is described by the following equation:

ρgdSdh = pdS−(p+dp)dS

Here, p represents the pressure, dp is the change in pressure, dS is the differential surface area, ρ is the density of the fluid, g is the acceleration due to gravity, and dh is the change in height.

This equation can be rearranged to yield the fluid-static equation:

−ρg = dp / dh (Equation 5)

This equation expresses the relationship between the change in pressure (dp / dh​) with respect to the change in height (dh), and the density of the fluid (ρ) and the acceleration due to gravity (g). It illustrates how pressure changes with altitude in a fluid at rest under the influence of gravity.

ISA equations

To obtain variations of density (ρ) and pressure (p) with altitude in the different layers of the atmosphere, we can use the equations provided in Hypothesis (2.1) and the fluid-static equation (Equation 5).

Troposphere

In the troposphere (0 ≤ h < 11000 m), introducing Equation (2.1) and Equation (2.2) into Equation (5) yields:

dp​ / dh=(p​/R(T0​−αh))g

Integrating between a generic altitude ℎ and sea level altitude (ℎ=0), the variation of pressure with altitude is given by:

p/p_o​​=(1−(α​/T₀)​h)^Rαg

​Using the pressure value from Equation (2.7) and substituting it into the perfect gas equation (Equation 2.1), the variation of density with altitude is:

p/p_o=(1−(α​/T₀)​h)^1-Rαg

Substituting the numerical values, we have:

T [K]=288.15−0.0065h [m]

ρ [kg/m3]=1.225(1−22.558×10^-6h [m])^4.2559

p [Pa]=101325(1−22.558×10^-6h [m])^5.2559

Warm and cold atmospheres

For warm and cold days, adjustments are made to the international standard atmosphere, resulting in what is known as the warm (ISA+5, ISA+10, ISA+15, etc.) and cold (ISA-5, ISA-10, ISA-15, etc.) atmospheres. These adjustments represent the difference in temperature compared to the standard temperature of 288.15 K for an average day.

Given the new temperature ( T₀ ) for a warm or cold day, and assuming that the pressure at sea level ( p₀ ) remains constant, the new density at sea level can be calculated. Then, the ISA equations are derived in the same manner as for the international standard atmosphere, using the adjusted temperature ( T₀ ) and the new density at sea level. This allows for the determination of pressure, density, and temperature at different altitudes for warm and cold atmospheric conditions.

Barometric altitude

Altitude determination based on atmospheric pressure measurement remains a common practice in aviation, with barometric altimeters being the primary tool used for this purpose. These altimeters, however, cannot adjust for variations in air temperature, which can lead to errors in indicated altitude when compared to the International Standard Atmosphere (ISA) model.

Barometric altimeters typically measure atmospheric pressure using an aneroid or mercury barometer from a static port located outside the aircraft, with reference to a standard pressure setting. According to the pressure ratio equation (Equation 16), and considering a reference pressure (pref), the altitude (h) and reference altitude (href) can be determined.

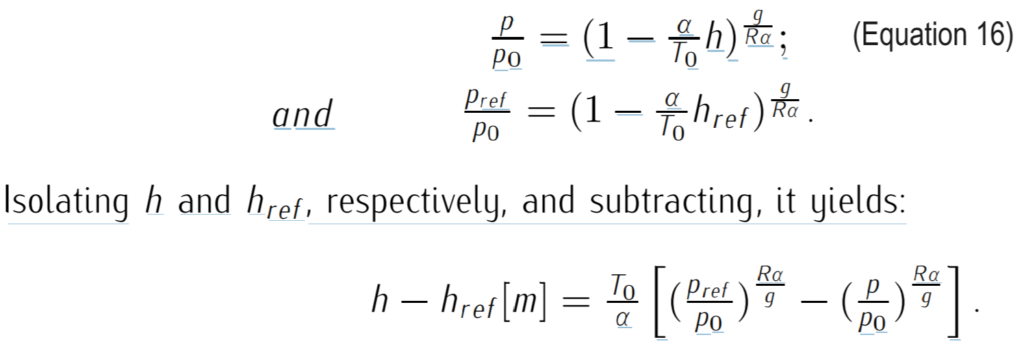
There are three main standards for setting the reference pressure:

1. QNE setting: Baseline pressure is set to 101325 Pa, equivalent to the air pressure at mean sea level (MSL) in the ISA model.
2. QNH setting: Baseline pressure is the actual pressure at sea level, which may deviate from 101325 Pa. The real pressure at sea level is estimated based on the measured pressure at the airfield, accounting for deviations from the ISA model.
3. QFE setting: The reference pressure (pref) is set to the pressure at the airport, making h – href reflect the altitude above the airport.

Each setting provides a different perspective on altitude and is used in different contexts depending on the requirements of the flight and local atmospheric conditions.