This article covers the basics of electromagnetic and black-body radiation, essential for grasping the characteristics of the Sun and the solar radiation reaching Earth. It also introduces key terms relevant for practical use of solar radiation.

What is Solar Radiation?
The source of solar energy
The Sun, our nearest star, is a spherical body primarily made up of hydrogen gas. It sits at the center of our solar system, about 150 million kilometers away from Earth. Within the Sun’s core, the intense gravitational pressure triggers nuclear fusion, converting hydrogen into helium and releasing vast amounts of electromagnetic radiation. This solar radiation makes the Sun the primary source of energy in our solar system. The Sun has various layers, from the dense inner core to the outer corona. Both the core and the corona are extremely hot, reaching temperatures of millions of degrees Kelvin, while the layers in between are cooler, though still quite hot by Earth’s standards.
The energy produced by fusion reactions in the Sun’s core is carried outward through a series of processes, including convection, radiation, absorption, emission, and re-radiation. Eventually, this energy reaches the photosphere, which acts as the Sun’s visible surface and emits a continuous spectrum of radiation. The photosphere is where most of the visible light that reaches Earth originates. Its temperature, known as the effective black-body temperature, is approximately 5777 Kelvin. Despite having multiple layers and a temperature gradient, the Sun behaves similarly to an ideal black-body radiator, which we’ll delve into in the next section.
Planck’s radiation law
Understanding the solar radiation reaching Earth involves grasping some basic concepts of electromagnetic radiation and the characteristics of black-bodies. Electromagnetic radiation behaves like waves, with each wave having a specific wavelength (λ). All electromagnetic radiation travels at the speed of light in a vacuum and has a frequency (ν) such that the product of wavelength and frequency equals the speed of light. Quantum mechanics also views electromagnetic radiation as a flux of particles called photons, where the energy of each photon depends on its frequency. For a specific wavelength, λ, the energy of a photon is given by E = hν = hc/λ, where h is Planck’s constant.
When an object, like the Sun, emits solar radiation due to its high temperature, this radiation covers a range of wavelengths, resulting in a flux of photons with varying energy. This emission pattern can be approximated using a theoretical construct called a black-body, which absorbs all incident radiation and emits the maximum possible amount of radiation at each wavelength. Planck’s radiation law describes the distribution of emitted radiation from a black-body at temperature T. This distribution depends on both quantum mechanics and thermodynamics and is given by an equation involving various constants and the temperature of the black-body.
Several fundamental relationships arise from Planck’s law. Wien’s displacement law states that the wavelength corresponding to the maximum emission shifts inversely with temperature, while the Stefan-Boltzmann equation reveals that the total emitted power increases with temperature to the fourth power. These principles explain why heated objects appear brighter as they get hotter.
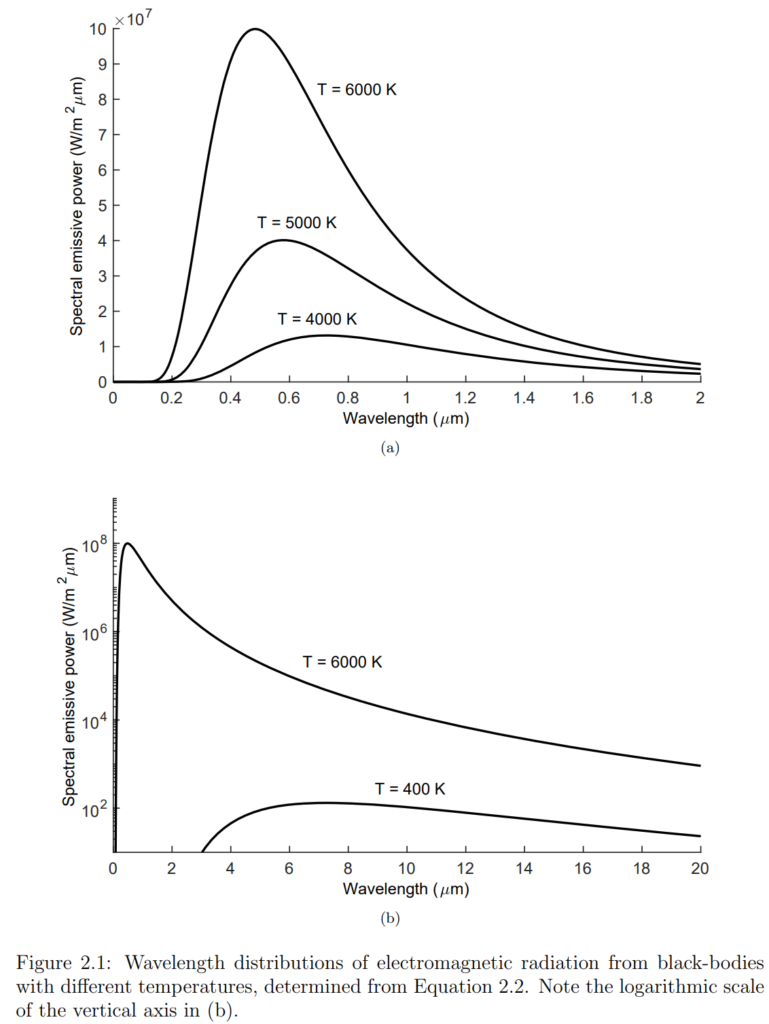
Figures illustrating these concepts show the spectral distribution of thermal radiation from a black-body at different temperatures. For instance, a black-body at 6000 Kelvin (the approximate surface temperature of the Sun) emits radiation differently from one at 400 Kelvin (close to typical daily temperatures). These visualizations help to understand how temperature affects the solar radiation emitted by objects, including the Sun.
The solar constant
The solar radiation reaching Earth’s atmosphere varies depending on the distance from the Sun. This variation follows the inverse square law, meaning that radiation levels decrease with the square of the distance from the Sun. To understand this, let’s consider the Sun as a source of radiation. Its surface area is 4πr², where r is the radius, and the total radiative flux from the Sun, calculated using the Stefan-Boltzmann equation, is σT⁴ × 4πr², where σ is the Stefan-Boltzmann constant and T is the temperature of the Sun’s surface.
Now, imagine a sphere with a larger radius, l, with the Sun at its center. The surface area of this sphere is 4πl². Despite the larger area, the same amount of solar radiation is distributed over it. Therefore, the energy flux per unit area at a distance l from the Sun is given by:
Gl = σT⁴ × 4πr² / 4πl² = σT⁴ × (r/l)².
Using the known values for the temperature of the Sun’s surface (5777 K), the radius of the Sun (6.957 × 10⁸ m), and the distance between the Sun and Earth (1.495 × 10¹¹ m), we can calculate the average radiative flux just outside Earth’s atmosphere, per unit area facing the Sun. This value is approximately 1367 W/m² and is referred to as the solar constant or air mass zero (AM0) radiation.
The solar constant (Gsc) isn’t determined directly by measuring the Sun’s surface temperature. Instead, it’s the other way around: scientists infer the temperature of the Sun’s surface by measuring Gsc at Earth. This is done using Equation 2.6, which is solved for the black-body temperature (T). Over time, estimates of Gsc have improved as researchers have made radiation measurements outside Earth’s atmosphere using aircraft, balloons, and spacecraft. The widely accepted value of 1367 W/m², adopted by the World Radiation Center (WRC), is commonly used in solar engineering literature.
By measuring solar radiation, scientists can also determine the spectral distribution of the AM0 radiation. Figure 2.2 illustrates the standardized WRC spectral irradiance curve, derived from high-altitude and space measurements. The spectral distribution of AM0 radiation closely resembles the shape of the black-body radiation curve obtained from evaluating Planck’s law near the surface temperature of the Sun (as seen in Figure 2.1). Any differences in the spectral distributions are primarily due to absorption in the cooler upper parts of the Sun’s photosphere.
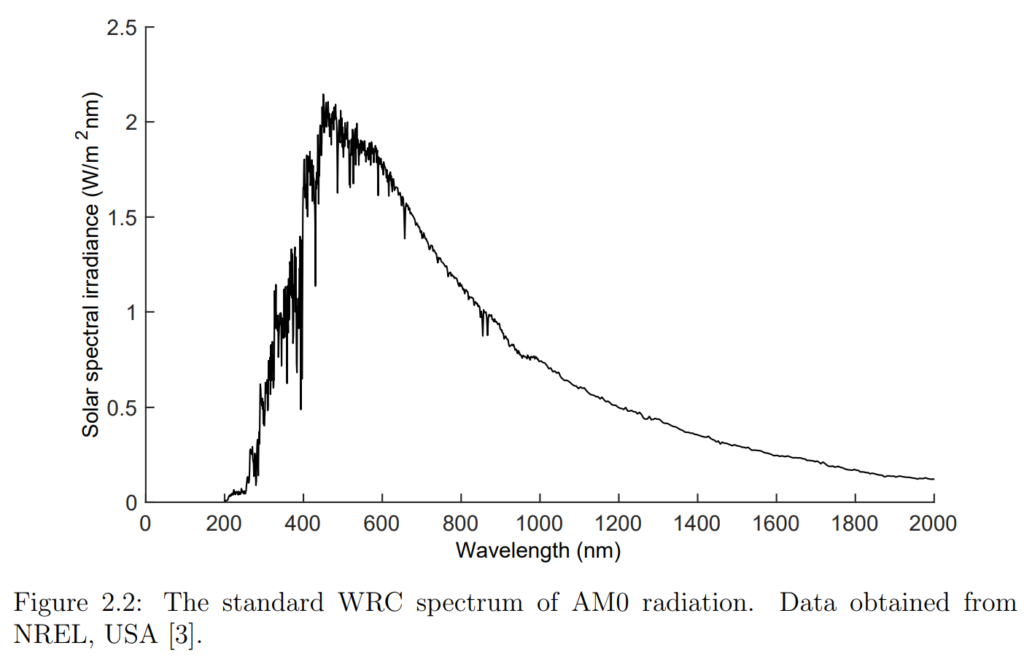
Due to Earth’s elliptical orbit around the Sun, the actual solar radiation outside the atmosphere at any given time, known as extraterrestrial radiation, differs from the solar constant (Gsc). Throughout the year, this radiation varies from approximately 1412 W/m² at the beginning of July to about 1322 W/m² at the turn of the year, representing a 3.3% fluctuation from the mean value. Mathematically, this variation can be expressed using the equation:
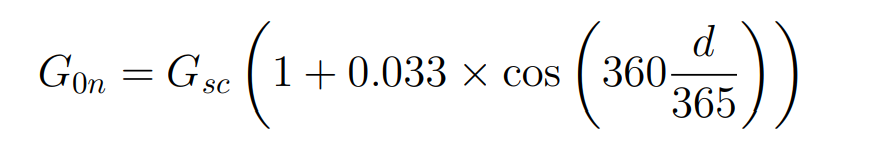
Here, ( d ) represents the day of the year. The subscript ( 0 ) indicates zero air mass (AM0) radiation, while the subscript ( n ) denotes that the radiation is measured on a plane normal to the Sun-Earth axis.
Solar Radiation Types
Electromagnetic radiation is divided into various wavelength bands based on its properties and applications. Figure 2.3 illustrates some common classifications relevant to solar engineering. The majority of solar radiation falls within the wavelength range of approximately 0.3 to 3 µm, covering parts of the ultraviolet (UV) and infrared (IR) spectra. For simplicity in solar engineering, wavelengths are often classified as either short-wave or long-wave radiation. Short-wave radiation corresponds to solar radiation, while long-wave radiation encompasses wavelengths longer than those of solar radiation. This division is advantageous for solar collectors because the properties of materials and devices can be tailored separately for short-wave solar and long-wave thermal radiation, as they do not significantly overlap.
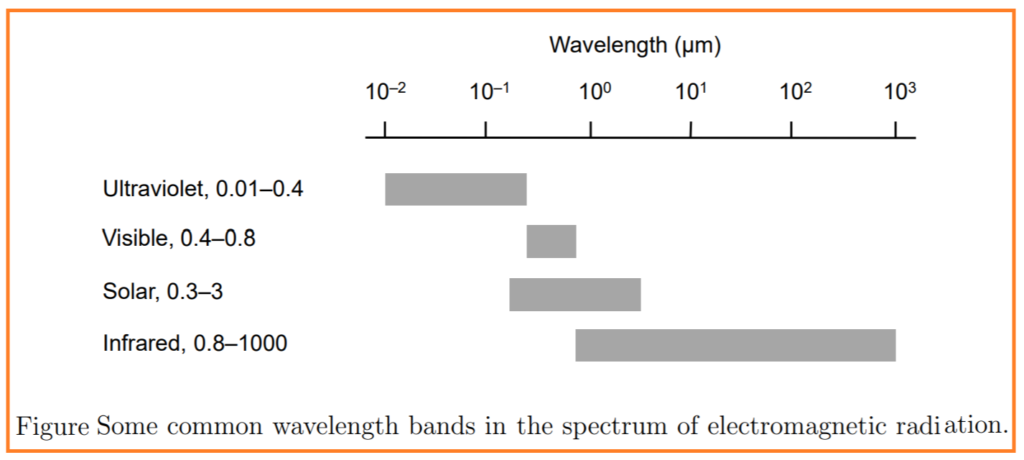
Available solar radiation on Earth
Extraterrestrial radiation undergoes several transformations as it traverses through Earth’s atmosphere. This section outlines these changes and elucidates the characteristics of the solar radiation reaching Earth’s surface. Additionally, a brief overview of Earth’s radiation and energy balance is provided.
1. Atmospheric attenuation
As solar radiation travels through Earth’s atmosphere, it encounters two main processes that reduce its intensity: scattering and absorption. Scattering happens when the radiation interacts with particles like air molecules, water droplets, and dust in the atmosphere. The extent of scattering depends on factors such as the wavelength of the radiation, the size and concentration of particles in the atmosphere, and the distance the radiation travels through the air. Rayleigh scattering is the most significant type, particularly affecting shorter wavelengths in the blue spectrum (less than 0.6 µm). This scattering phenomenon is responsible for the blue color of the sky during the day, the yellow hue of the Sun, and the reddish tint of the sky at dusk and dawn. Notably, a portion of the scattered light is directed back into space.
Absorption occurs predominantly in the ultraviolet (UV) range due to ozone and in the infrared (IR) range due to water vapor and carbon dioxide. During absorption, solar radiation is converted into heat, which is then emitted as long-wave radiation by the absorbing particles.
Rayleigh scattering has a significant impact on solar radiation and varies with wavelength, as illustrated in Figure 3.1.

2. Air mass
The Attenuation of solar radiation is weakened depends on how far it has to travel through the atmosphere. Longer distances mean more interactions with atmospheric particles. This distance varies throughout the year and even within a single day, with the longest path occurring during sunset and sunrise when the Sun is near the horizon. This path length is quantified by a value called air mass.
Air mass represents the ratio of the atmospheric mass the sunlight traverses from the Sun’s current position in the sky to the mass it would traverse if the Sun were directly overhead (at the zenith). For instance, an air mass of 2 indicates that the path through the atmosphere is twice as long as it would be if the Sun were directly overhead.
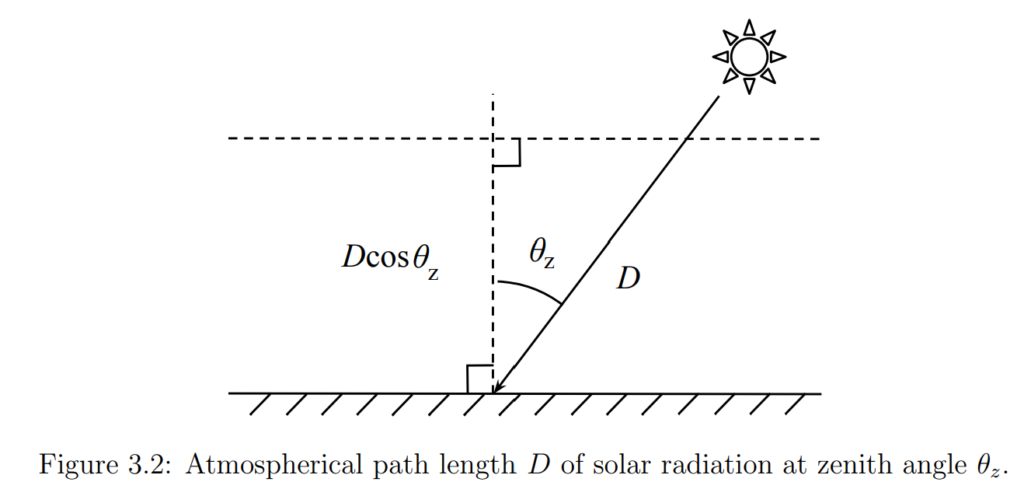
The relationship between air mass and the zenith angle (the angle from directly overhead to the Sun) is given by the formula:
m=1/cosθz
where ( θz ) is the zenith angle. This formula is valid for zenith angles less than 70 degrees (as shown in Figure 3.2), beyond which the curvature of the Earth starts to influence the calculation. At a zenith angle of 85 degrees, for example, there’s approximately a 10% error due to this curvature effect.
Since atmospheric conditions fluctuate, a standardized spectrum for ground-level radiation is essential for the development and testing of solar devices. The widely accepted standard is the AM1.5 spectrum, which corresponds to an air mass of 1.5, equivalent to a zenith angle of approximately 48.2 degrees. Figure 3.1 depicts the AM1.5 spectrum alongside the extraterrestrial WRC spectrum and a 6000 K black-body distribution for comparison.
3. Solar Radiation components
On Earth’s surface, incoming solar radiation consists of two main components due to scattering in the atmosphere. Some of the incoming radiation remains as beam radiation, following a well-defined direction from the Sun to the surface. However, a portion of the radiation scatters in the atmosphere and is either reflected back into space or reaches the ground as diffuse radiation. Unlike beam radiation, which comes from a specific direction, diffuse radiation originates from all parts of the sky. Although diffuse solar radiation is most intense near the Sun, it’s often treated as isotropic, meaning it’s uniformly distributed in all directions.
The proportions of diffuse and beam radiation vary significantly depending on weather conditions. On clear, sunny days, roughly 10-20% of the radiation reaching the surface is diffuse. In contrast, on cloudy days with limited sunshine, the majority of the incoming radiation is diffuse. Figure 3.3 illustrates these variations on two different days in Norrköping, Sweden. Over the course of a year, the total diffuse radiation can be substantial. For instance, in Norrköping, the average diffuse portion of total radiation between 1983 and 1998 was 51%, while even in one of Sweden’s sunniest locations, Visby, it remained at 47% during the same period.
Furthermore, diffuse radiation exhibits a different spectral distribution compared to beam radiation. The higher frequency part of the spectrum is more pronounced due to Rayleigh scattering, which predominantly affects shorter wavelengths. However, for most practical applications, the spectral distribution of diffuse radiation is often assumed to be similar to that of beam radiation.
A third component to consider in solar energy applications is the radiation reflected from the ground and surrounding objects onto sloped surfaces. This component depends on the reflectivity of the ground, known as albedo.

4. Temporal and geographical variations in solar energy availability
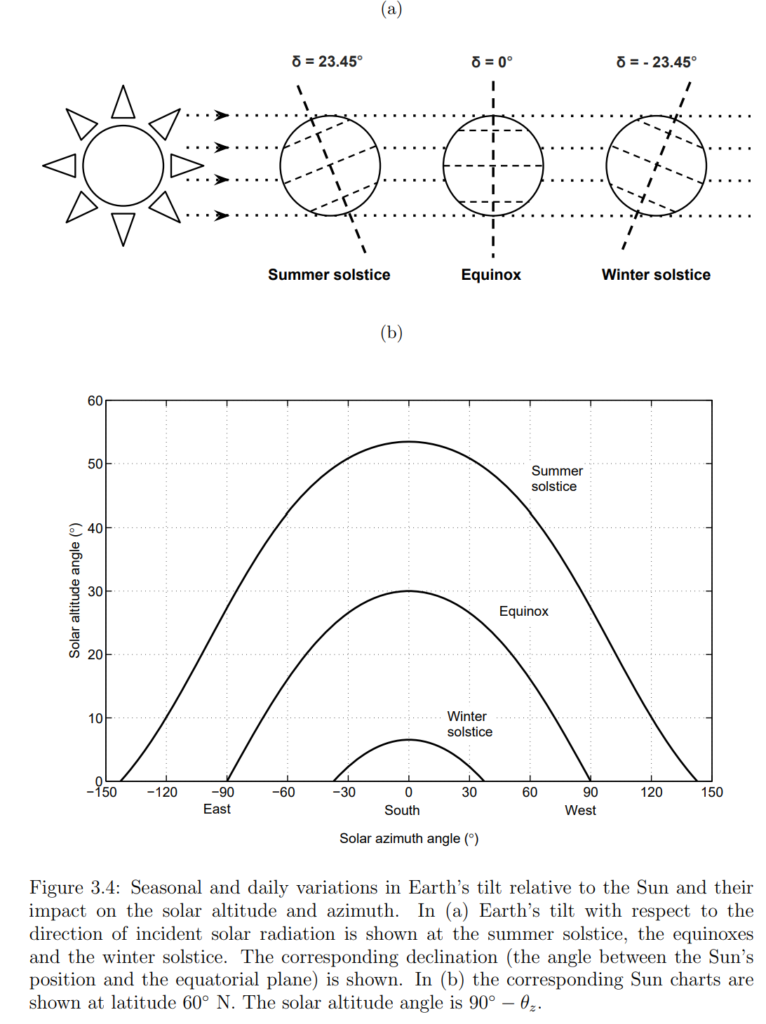
Solar energy variability plays a fundamental role in the Earth’s climate and ecosystems, primarily driven by the tilt of Earth’s axis relative to its orbit around the Sun. This axial tilt gives rise to seasonal variations in solar energy availability, resulting in the familiar cycle of seasons. Additionally, Earth’s rotation on its axis leads to the alternation of day and night.
During the summer solstice, the Northern Hemisphere is tilted most directly toward the Sun, resulting in the longest day of the year, while the winter solstice sees the Northern Hemisphere tilted away from the Sun, leading to the shortest day of the year. Equinoxes, occurring between the solstices, mark the times when Earth’s axis is perpendicular to the Sun, resulting in equal day and night lengths for both hemispheres.
The movement of the Sun across the sky also varies daily and seasonally, affecting the duration and intensity of solar radiation received at different latitudes. At higher latitudes, such as 60°N, the Sun reaches its highest position in the sky during the summer solstice and its lowest during the winter solstice. Equinoxes, on the other hand, see the Sun rising exactly in the east and setting exactly in the west.
These seasonal and daily variations in solar energy are predictable and form the basis of mathematical models used in solar engineering.
In addition to these predictable variations, solar energy availability is also influenced by short-term factors such as cloud movements and atmospheric transparency. Cloud cover can lead to significant short-term fluctuations in solar irradiance, but these variations tend to even out over longer periods. Clear-sky irradiance data can be used to normalize solar radiation variability due to cloudiness, allowing for quantification of the clear-sky index.
While solar irradiance varies over time and location, certain measures remain consistent when averaged over longer periods. For instance, the ˚Angstr¨om equation relates total irradiation over a period, total clear-sky irradiation, and the fraction of bright sunshine hours relative to the total potential sunshine hours.
Geographically, solar resource availability varies with latitude, with more solar energy available closer to the equator and less toward the poles. However, local climate, weather, and terrain conditions also play significant roles, with coastal regions generally receiving more solar energy than mountainous areas.
5. Earth’s energy balance
Solar radiation is indeed the primary energy source driving processes on Earth. While other energy sources such as geothermal and tidal energy exist, the flux of solar energy far surpasses them. Approximately 130,000 gigatonnes of oil equivalents (Gtoe) of solar energy reach Earth annually, dwarfing the contributions from geothermal and tidal energy, which amount to 19 Gtoe and 2 Gtoe, respectively.
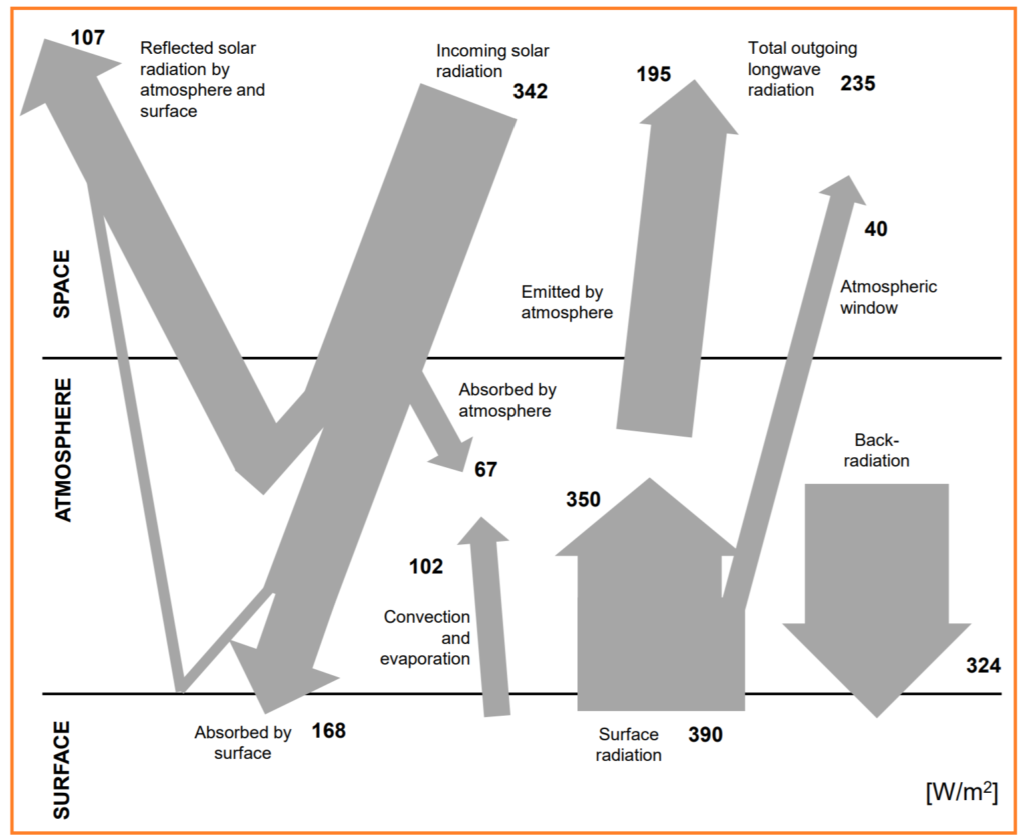
An intricate energy balance exists between incoming solar radiation and outgoing radiation from Earth. About one-third of the incident solar energy is reflected back into space, while the remainder is absorbed by various components of Earth’s system, including the atmosphere, oceans, and land. This absorbed energy drives meteorological, hydrological, and biological processes vital for sustaining life on Earth.
The balance of incoming and outgoing solar radiation is crucial for maintaining Earth’s climate and temperature. Greenhouse gases in the atmosphere play a key role in this balance by trapping some of the outgoing long-wave radiation emitted by Earth’s surface, which helps regulate temperatures. However, increased concentrations of greenhouse gases, such as carbon dioxide and water vapor, can lead to the narrowing of the atmospheric window, causing concerns related to global warming and climate change.
Understanding the spectral selectivity of ambient radiation and natural systems’ responses to it is essential for engineering solar devices. Solar engineers can leverage this knowledge to design efficient and effective solar energy technologies that harness the abundant energy from the Sun while mitigating environmental impacts.