What is Bernoulli effect? Bernoulli Equation, Formula & Derivation

The Bernoulli Equation tells us that when a fluid flows through a constriction, its speed increases, and when it exits the constriction, its speed decreases back to its original level. This principle is explained by the Bernoulli effect, which states that fluid flows faster where the pressure is lower.

What is Bernoulli effect?

To understand this, imagine water flowing through a narrow nozzle. As the water enters the nozzle, it speeds up because the cross-sectional area decreases. This means that the pressure in the nozzle decreases because the fluid is moving faster. When the water exits the nozzle, its speed decreases, and the pressure increases back to its original level.

The Bernoulli effect: Fluid flows faster where the pressure is lower.

The Bernoulli effect can seem counterintuitive because we might expect rapidly moving fluid to have high pressure. For example, if you’re hit by water from a firehose, you might think the pressure is high because it knocks you over. However, the high pressure is only felt when the water slows down or stops, causing its pressure to increase dramatically. When the water is moving quickly, as in the jet from the hose, its pressure is actually close to atmospheric pressure.

Bernoulli Equation, Formula & Derivation

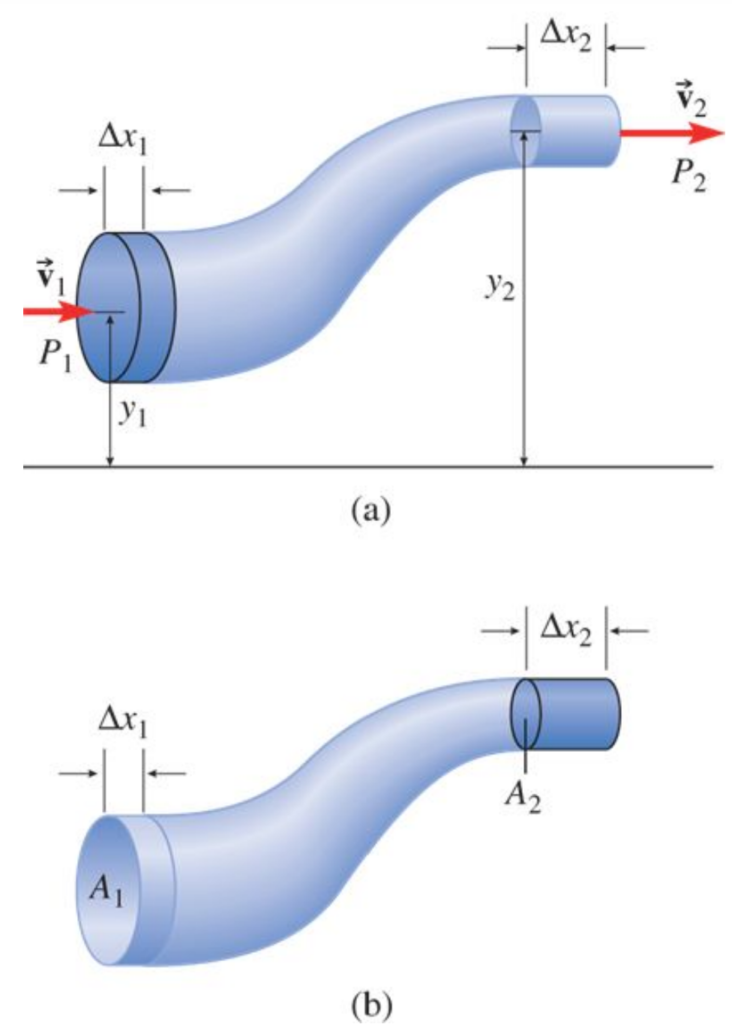
Let’s explore the quantitative relationship between changes in pressure and flow speed for an ideal fluid. In the figure, the shaded volume of fluid flows to the right. If the left end moves a distance Δx1​, then the right end moves a distance Δx2​. Since the fluid is incompressible.

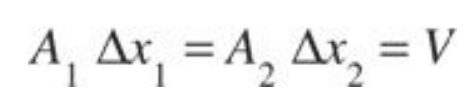
Work is done by the neighboring fluid during this flow. The fluid behind (to the left) pushes forward, doing positive work, while the fluid ahead pushes backward, doing negative work. The total work done on the shaded volume by the neighboring fluid is given by the expression:

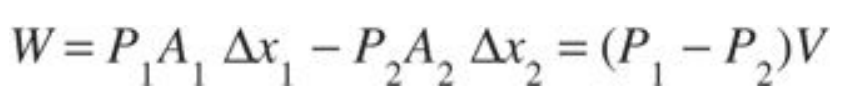
Since no dissipative forces act on an ideal fluid, the work done is equal to the total change in kinetic and gravitational potential energy. The net effect of the displacement is to move a volume ( V ) of fluid from height ( y₁ ) to height ( y₂ ) and to change its speed from ( v₁ ) to ( v₂ ). The energy change is therefore given by:

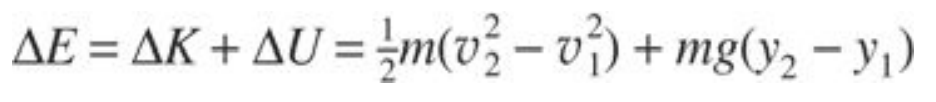
m=V and equating the work done on the fluid to the change in its energy yields:

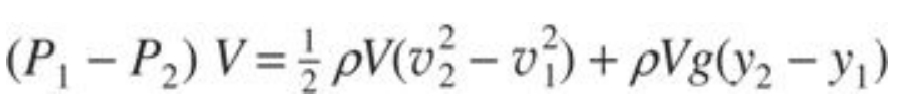
Bernoulli’s equation (for ideal fluid flow):

Bernoulli’s equation is a fundamental principle in fluid dynamics that describes the conservation of energy along a streamline in an ideal fluid flow. It relates the kinetic energy, potential energy, and pressure of the fluid at two points along the streamline. This equation is applicable in various scenarios, ranging from simple pipe flows to complex aerodynamic situations, as long as the assumptions of inviscid, incompressible flow hold true.

Each term in Bernoulli’s equation represents work or energy per unit volume. Here’s a breakdown of the units and the physical interpretation of each term:

1. Pressure (p): The pressure term represents the work done by the fluid on the fluid ahead of it per unit volume of flow. It has units of pascals (Pa) or newtons per square meter (N/m²), which are equivalent to joules per cubic meter (J/m³).
2. Kinetic Energy per Unit Volume (½ρv²): This term represents the kinetic energy of the fluid per unit volume. It has units of energy per unit volume, which in the SI system is joules per cubic meter (J/m³).
3. Gravitational Potential Energy per Unit Volume (ρgy): This term represents the gravitational potential energy of the fluid per unit volume. It has units of energy per unit volume, which again is joules per cubic meter (J/m³).

By considering these terms in Bernoulli’s equation, we can understand how the pressure, velocity, and elevation of a fluid are interconnected and how changes in one affect the others in a flow system.