What is Process Engineering?

Process engineering is a branch of engineering that focuses on the design, operation, optimization, and control of industrial processes used to produce goods or services. It involves applying principles from various fields of science and engineering to develop efficient and reliable processes for transforming raw materials into desired products.

What is Process Engineering?

The distinguishing feature of process engineering is its focus on the development, design, and operation of various processes. While the public may associate chemical engineers with the production of chemicals, their work extends far beyond that to include a wide range of industries and applications.

Process engineers typically work in three types of organizations:

1. Operating Companies: These are companies like DuPont and Dow Chemical that focus on producing products. They are also involved in developing new processes to improve their operations.
2. Plant Construction Organizations: Companies like C.E. Lummus Corp. or Forster Wheeler Corp. are contacted when a new plant for an improved or newly developed process is needed. They specialize in building and constructing these plants.
3. Supporting Companies: Many companies provide consulting services and manufacture equipment needed for chemical processes, such as pumps, heat exchangers, and distillation columns. They support the activities of operating and plant construction companies.

It’s important to note that many companies may be involved in more than one of these activities, making classification sometimes difficult. Overall, chemical engineering encompasses a broad range of industries and activities, all centered around developing and optimizing processes for various applications.

PROCESS TYPES

There are many different kinds of processes, and it can be hard to put them into categories. But it’s important to try, so we can understand how industries work. Some experts, like Wei et al., have talked about how chemical industries are structured. Magazines like Chemical Engineering also give their own classifications. The U.S. Bureau of Budget has a system called NAICS for classifying industries. They have a list of different process types based on what they make, which shows how diverse processes can be.

One type of process listed is chemical intermediates. These are chemicals used to make other chemicals, but they’re not usually sold directly to the public. For example, ethylene is an intermediate made from gases like natural gas or petroleum. Then, ethylene is used to make things like polyethylene, a type of plastic, as well as other products like vinyl chloride and styrene. There are a lot of different chemicals classified as intermediates.

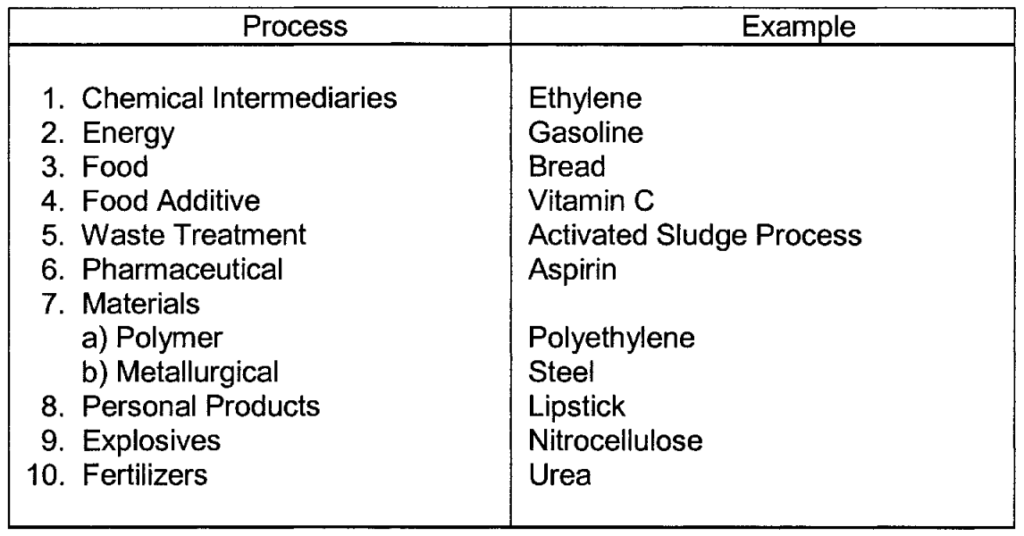
Energy Processes Examples

Energy processes include things like making fuel from petroleum or generating electricity in a steam power plant. While we don’t usually think of a power plant as a process, it actually is. A steam power plant has equipment like furnaces, pumps, fans, and heat exchangers. It also has systems for treating water and cleaning the smoke before it goes out into the air. Power plants are usually run by mechanical and electrical engineers, but chemical engineers can also work there because they understand how chemical processes work. Even though power plants have a lot of mechanical and electrical stuff, chemical plants also have some of this equipment. For example, in a process to make methanol, there are steam turbines used to recover energy.

Bread making is another kind of process, and it’s mostly mechanical. But it also involves fermentation, where yeast turns flour into bread. This means bread making is also a biochemical process. Another process, the activated sludge process, uses microorganisms to clean up water by eating organic pollutants and turning them into harmless stuff like carbon dioxide and water. Then the microorganisms are separated from the water, and some are used again while the rest is thrown away.

Aspirin is one of the oldest medicines around, and it’s been made for over a hundred years. It was discovered by a chemist named Felix Hoffmann, who worked for a company called Bayer in Germany. He was trying to find something to help his dad’s rheumatism pain, but aspirin turned out to be useful for lots of other things too, like preventing heart attacks and strokes.

Process Systems Engineering (PSE)

Process Systems Engineering (PSE) is all about engineering systems that involve physical, chemical, and/or biological processes. While the engineering of processing systems has been around since the start of the industrial revolution, the term PSE was only coined about 50 years ago when computer-aided engineering became more prevalent.

In recent years, PSE has grown beyond its original focus on continuous and batch chemical processes. Now, it includes designing, operating, and controlling biological systems, complex networks of chemical reactions, self-assembly processes, and even processes at the micro- and nano-scale. It also extends to energy systems that use renewable sources and managing global supply chains for fuels and chemicals, considering environmental and life cycle issues.

Process modeling in PSE

In Process Systems Engineering (PSE), modeling plays a crucial role in understanding and solving real-world problems. Here’s a breakdown of what modeling entails:

• Definition of a Model: A model is essentially a simplified representation of reality. When we talk about mathematical models, we’re referring to a specific type of representation that uses mathematical equations to describe real-world phenomena.
• Purpose of Model Building: The process of building a model involves translating a real-world problem into a mathematical framework that we can solve and interpret. We do this to gain insights into the original problem or to use the model for tasks like control, optimization, or safety studies.
• Nature of Process Engineering Models: In the field of process engineering, the models we work with are primarily mathematical. They aim to capture certain aspects of a system through equations, tailored for specific uses of the model.
• Characteristics of a Good Model: When building a model, we aim to represent key characteristics of the actual system. These characteristics include:
  • Ensuring that the outputs of the model respond correctly as the inputs change.
  • Establishing a valid structure that accurately represents how inputs, outputs, and internal variables are connected.
  • Ensuring that the model exhibits the correct short-term and/or long-term behavior, as observed in the real system.

Modeling Steps

Step 1: Reality to Mathematics

In the initial step of translating reality into mathematics, several key considerations need to be addressed:

1. Understanding the Real Problem: It’s essential to have a clear understanding of the real-world problem we’re trying to model. This involves identifying the relevant factors, processes, and interactions at play.
2. Intended Use of the Model: We need to define the purpose of the mathematical model. Is it for gaining insights, making predictions, optimizing processes, or something else? The intended use will guide how the model is developed and applied.
3. Governing Phenomena or Mechanisms: Identify the fundamental principles or mechanisms that govern the behavior of the system. This could include physical laws, chemical reactions, biological processes, etc.
4. Form of the Model: Determine the appropriate form or structure of the mathematical model based on the nature of the system and its behavior. This could range from simple algebraic equations to complex differential equations or stochastic models.
5. Model Structure and Documentation: Establish how the model will be organized and documented to ensure clarity, reproducibility, and ease of interpretation. This includes defining variables, parameters, assumptions, and relationships within the model.
6. Accuracy Requirements: Define the level of accuracy required for the model based on its intended use and the significance of its predictions or outcomes. This will influence the complexity and detail of the model.
7. Data Availability and Quality: Assess the availability, quality, and accuracy of data needed to build and validate the model. This involves identifying sources of data, evaluating their reliability, and addressing any gaps or uncertainties.
8. System Inputs, States, Outputs, and Disturbances: Clearly define the inputs that influence the system, the internal states of the system, the desired outputs or responses, and any external disturbances or perturbations that affect the system’s behavior.

Addressing these considerations systematically helps ensure that the mathematical model accurately represents the real-world system and fulfills its intended purpose effectively.

Step 2 – Mathematical Solution

In the mathematical solution phase, we aim to solve the mathematical description of the real-world system to determine the values of the variables representing that system. Here are the key issues to consider:

1. Choice of Variables: Selecting the appropriate variables in the model to satisfy the degrees of freedom, ensuring that the model is well-defined and solvable.
2. Solubility of the Model: Assess whether the model is solvable, considering the complexity of the equations and the availability of numerical or analytical solution techniques.
3. Solution Techniques: Determine the most suitable numerical or analytical solution technique to solve the model equations effectively. This could involve methods like numerical integration, optimization algorithms, or analytical approaches.
4. Exploiting Problem Structure: Explore whether the structure of the mathematical problem can be exploited to improve solution speed or robustness. This may involve simplifying assumptions, reformulating equations, or utilizing problem-specific algorithms.
5. Representation of Results: Decide on the form of representation to display the solution results. This could include 2D graphs, 3D visualizations, contour plots, or other graphical representations to facilitate interpretation and analysis.
6. Sensitivity Analysis: Evaluate how sensitive the solution outputs are to variations in system parameters or inputs. Conduct sensitivity analysis to assess the impact of uncertainties or changes in model inputs on the results.

By addressing these issues, we can effectively solve the mathematical model and obtain meaningful insights into the behavior of the real-world system.

Model Classification

We can classify models in various ways, each highlighting different characteristics that influence solution techniques and application areas. Here are some common types of models and their basic characteristics:

1. Mechanistic Models: These are based on underlying mechanisms or phenomena governing the system.
2. Empirical Models: Derived from input-output data, trials, or experiments rather than underlying principles.
3. Stochastic Models: Include probabilistic elements, accounting for randomness or uncertainty in the system.
4. Deterministic Models: Rely on cause-effect analysis, where outcomes are determined by known inputs and conditions.
5. Lumped Parameter Models: Dependent variables are not influenced by spatial position, simplifying the representation of the system.
6. Distributed Parameter Models: Dependent variables vary with spatial position, providing more detailed spatial information.
7. Linear Models: Follow the superposition principle, where responses are directly proportional to inputs.
8. Nonlinear Models: Do not adhere to the superposition principle, often exhibiting complex, nonlinear relationships between inputs and outputs.
9. Continuous Models: Dependent variables are defined continuously over space and time, offering a smooth representation of the system’s behavior.
10. Discrete Models: Defined only for specific values of time and/or space, suitable for systems with distinct intervals or events.
11. Hybrid Models: Combine both continuous and discrete behaviors, allowing for a more comprehensive representation of complex systems.

Each type of model has its advantages and limitations, and the choice of model depends on the specific characteristics of the system being studied and the objectives of the analysis.