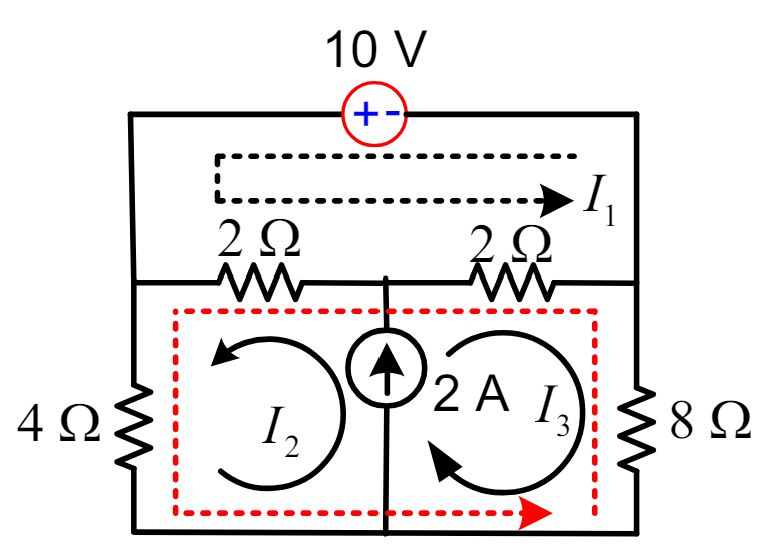
Supermesh Analysis is an extension of Mesh Current Analysis used to handle circuits with current sources that exist between two meshes. When you encounter such a current source, you form a “supermesh” by combining the meshes it affects. Here’s a guide on how to perform Supermesh Analysis:
When to Use Supermesh Analysis?
Use Supermesh Analysis when a current source lies between two meshes.
Steps for Supermesh Analysis:
- Identify the Meshes and Supermeshes:
- Label each mesh with a circulating current.
- Identify any current sources shared between two meshes. Combine these meshes into a supermesh.
- Write KVL Equations for the Supermesh:
- Write Kirchhoff’s Voltage Law (KVL) equations around the supermesh, excluding the current source.
- Write the Current Source Constraint Equation:
- Write an equation that represents the current source’s value as the difference between the two mesh currents it affects.
- Solve the System of Equations:
- Solve the combined KVL and current source constraint equations to find the mesh currents.
Example Circuit for Supermesh Analysis:
Determine the current Ix in below circuit diagram.
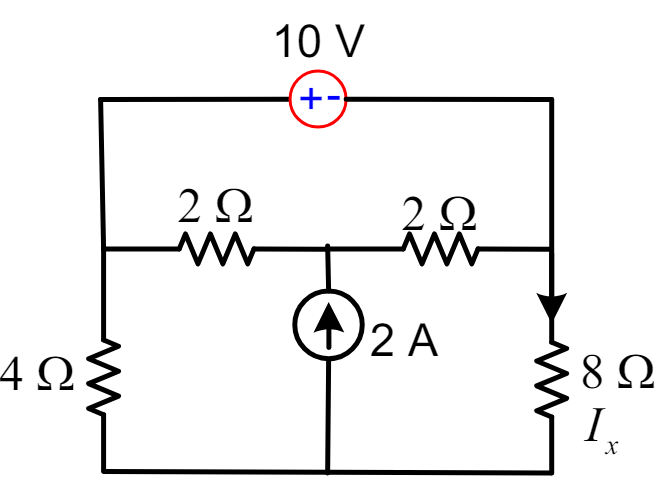
Solution:
Step 1: Need to identify meshes and supermeshes. Below picture shows label of each mesh with a circulating current. And combine these meshes into supermeshes.
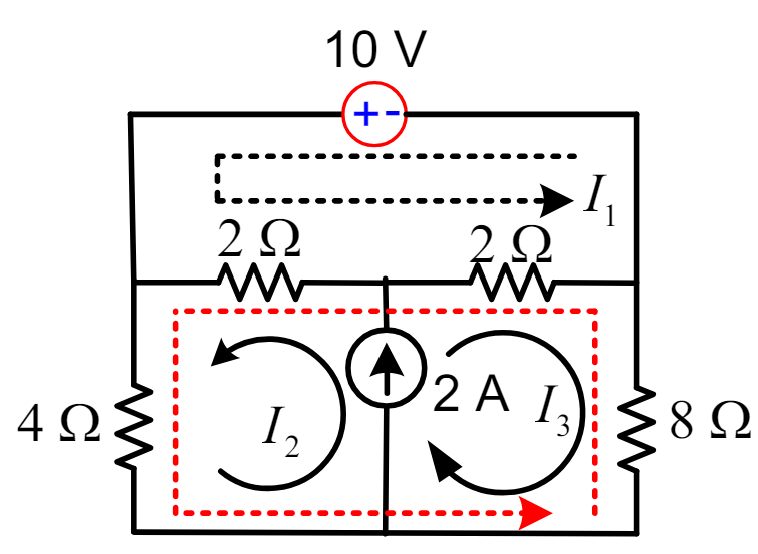
Step 2: Writing KVL Equations for the Supermesh circuits.
First derive KVL for I1 .
2 (I1 – I2 ) 2 (I1 + I3 ) – 10 = 0
4 I1 − 2 I2 + 2 I3 = 10 Equation – 1.
Supermesh KVL is below in equation.
4 I2 + 2(I2 − I1) + 2(− I3 − I1) − 8 I3 = 0
4 I1 + 6 I2 − 10 I3 = 0 Equation – 2.
As per supermesh rule of law.
I2 + I3 = 2 Ampere Equation 3.
Step 4: Solving the equations by cramer’s rule.
4 I1 − 2 I2 + 2 I3 = 10 4 I1 + 6 I2 − 10 I3 = 0 I2 + I3 = 2
Here i am mentioning direct result of equations by solving method of Cramer’s rule.
I1 = 3.667A I2 = 2.167A, I3 = 0.167A
so answer is of Ix is 0.167A.
FAQs about Supermesh Analysis.
Q1: What are the advantages of using Supermesh Analysis?
Supermesh Analysis simplifies the process of solving circuits with current sources between meshes by reducing the number of equations and avoiding direct voltage drops across current sources, leading to more straightforward calculations.
Q2: How does Supermesh Analysis relate to Mesh Current Analysis?
A: Supermesh Analysis is an extension of Mesh Current Analysis. It follows the same principles but includes additional steps to handle current sources between meshes, making it a more versatile method for complex circuits.
Q3: What if a circuit has multiple current sources between meshes?
If there are multiple current sources, you may need to create multiple supermeshes. Each supermesh should be treated individually, with its KVL equation and constraint equations for each current source.
Q4: Can Supermesh Analysis be used for both AC and DC circuits?
Yes, Supermesh Analysis can be used for both AC and DC circuits. The process remains the same, but for AC circuits, you need to account for complex impedances and phasors instead of just resistances and currents.
Q5: How do you handle current sources in a supermesh?
A: In a supermesh, you exclude the voltage drop across the current source when writing the KVL equation. Instead, you write a separate constraint equation that relates the mesh currents on either side of the current source.
Q6: What are the steps for performing Supermesh Analysis?
1. Identify and label all mesh currents in the circuit.
2. Identify any current sources that are shared between two meshes and form a supermesh.
3. Write the KVL equation for the supermesh, ignoring the current source.
4. Write a constraint equation for the current source.
5. Solve the system of equations to find the mesh currents.
Q7: How do you create a supermesh?
A: To create a supermesh, you effectively ignore the current source and combine the two meshes it affects into one larger loop. Then, you write a single KVL equation for this combined loop, excluding the voltage drop across the current source.
Q8: When should I use Supermesh Analysis?
A: Use Supermesh Analysis when you encounter a current source that is shared between two adjacent meshes. This method helps you avoid complications that arise from having a current source directly within the loops.
Q9: What is Supermesh Analysis?
A: Supermesh Analysis is a technique used in circuit analysis to handle current sources located between two meshes. By combining the meshes affected by the current source into a single supermesh, you can simplify the process of writing and solving the necessary equations.