Electromotive Force (EMF) is the electrical potential difference or voltage produced by a source such as a battery, generator, or cell. It is responsible for driving an electric current through a circuit. EMF is measured in volts (V). Despite its name, EMF is not a force but a potential energy per unit charge. It represents the work done on a unit positive charge as it moves through a circuit. EMF can be influenced by factors such as the type of energy source, chemical reactions, and the presence of an external circuit. PDF
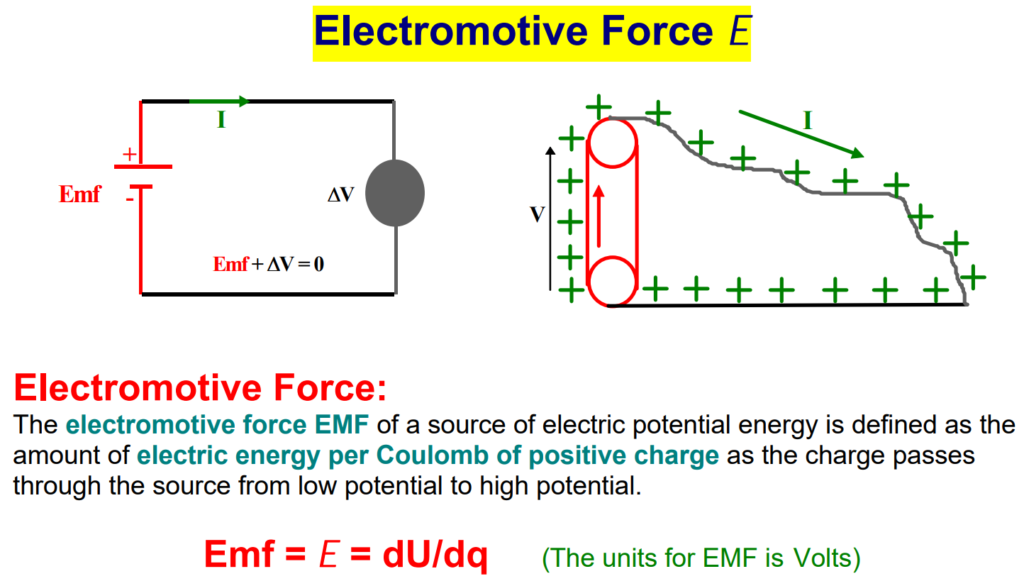
In simple terms, it is the force that drives electrons to flow in a closed circuit, creating an electric current.
A continuous flow of electric current in a closed circuit is sustained by an electromotive force (emf) provided by a source like a battery or generator, creating an electric field that propels charges through the circuit. The emf represents the work done per unit charge, measured in volts, making it the SI unit for emf. It is defined as the maximum voltage produced by the energy source.
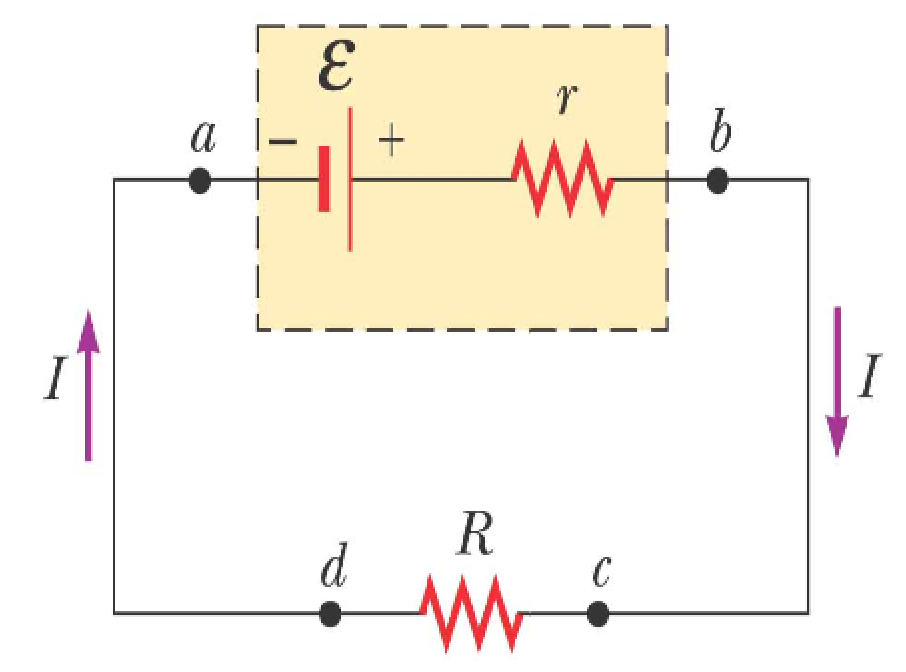
In the given figure, assuming the connecting wires have no resistance:
The positive terminal of the battery is at a higher potential than the negative terminal. In the absence of internal resistance in the battery, the potential difference across it, known as the terminal voltage, is equal to its electromotive force (emf).
However, real batteries always have some internal resistance denoted by ‘r.’ In a circuit with a current flowing, the terminal voltage is not equal to the emf due to this internal resistance.
In the provided figure, as we progress from the negative terminal to the positive terminal, the potential increases by an amount denoted as ε. When moving through the resistance ‘r’ in the circuit, the potential decreases by an amount represented by Ir, where ‘I’ is the current flowing through the circuit.
∆V=ε-Ir
The symbol ε represents the open-circuit voltage, which is equivalent to the terminal voltage when the current is zero. The electromotive force (emf) is the voltage labeled on a battery. The terminal voltage ‘V’ must be equal to the potential difference across the external resistance ‘R’, often referred to as the load resistance.
The resistor in the circuit symbolizes a load on the battery as the battery needs to provide energy to operate the device. The potential difference across the load resistance is given by ∆V = IR, where ‘I’ is the current flowing through the circuit, and ‘R’ is the load resistance.
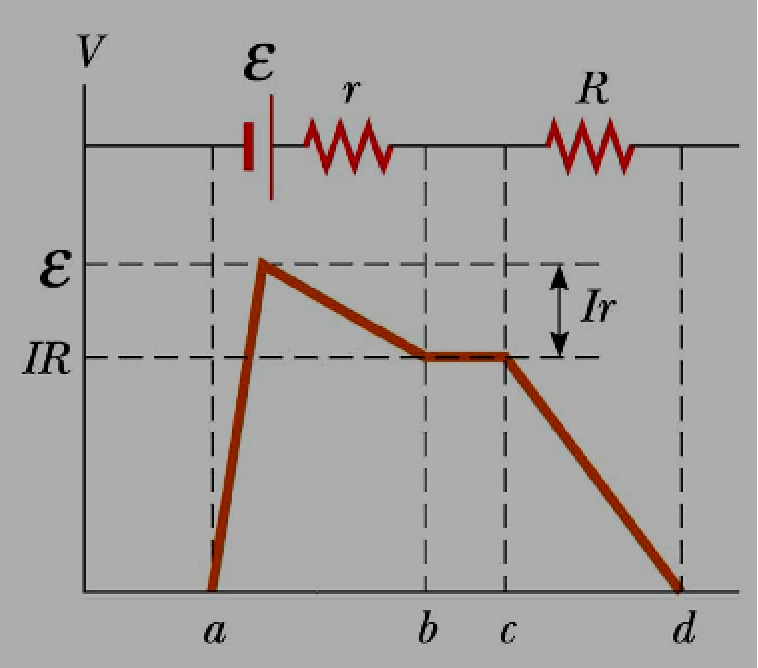
The total power output (Iε) of the battery is divided into two parts: one delivered to the external load resistance (I²R) and the other to the internal resistance (I²r).
Iε= I²R + I²r
Electromotive force formula
The formula for electromotive force (EMF) in an electrical circuit is typically represented by the symbol (ε) (epsilon). Mathematically, it is expressed as:
EMF(ε)=I⋅R+I⋅r
where:
- EMF (ε) ) is the electromotive force,
- ( I ) is the current flowing in the circuit,
- ( R ) is the external load resistance (also known as the load),
- ( r ) is the internal resistance of the source.
This formula takes into account both the voltage drop across the external resistance ((I . R)) and the voltage drop across the internal resistance ((I. r)), providing a comprehensive understanding of the overall potential in the circuit. It’s important to note that in an ideal scenario with zero internal resistance ((r = 0)), the formula simplifies to EMF(ε)=I⋅R.
EMF Calculation Example:
What is an Electromotive Force Symbol?
The symbol for Electromotive Force (EMF) is commonly represented by the letter “ε” (epsilon) in equations and electrical circuit diagrams.
What Is EMF Formula?
In a closed circuit, the EMF is equal to the potential difference across the terminals of the energy source when there is no current flowing I=0. However, when a current is present, the terminal voltage may differ due to internal resistance in the source. The relationship formula is often expressed as:
V=ε−Ir
where:
V is the terminal voltage,
ε is the electromotive force (EMF) of the source,
I is the current flowing through the circuit, and
r is the internal resistance of the energy source.
What Is the Unit of Electromotive Force?
Mathematically, EMF (ε) is given by the ratio of energy (measured in joules) provided by the source to the amount of electric charge (measured in coulombs) it moves. This relationship is encapsulated by the equation:
ε=Energy / Charge
In practical terms, EMF represents the maximum potential difference across the terminals of the source when no current is flowing (I=0). It characterizes the source’s ability to do work on the electric charges within the circuit, facilitating the movement of charge carriers.
Understanding the concept of EMF is crucial in the analysis and design of electrical circuits, as it provides insights into the driving force behind the flow of electric current. The unit of EMF is the volt (V), where 1 volt is equivalent to 1 joule per coulomb.
What Is the EMF and Difference between Terminal Voltage?
The difference between terminal voltage and electromotive force (EMF) lies in their definitions, measurement methods, occurrence scenarios, symbols used, and the consideration of real versus ideal cases. Terminal voltage, denoted as (V) or (Vt), refers to the potential difference across the terminals of a load when the circuit is active and current is flowing. This practical voltage is measured using a voltmeter, and it reflects the actual voltage considering factors like internal resistance and losses within the circuit.
On the other hand, electromotive force (EMF), often represented by the symbol (ε) (epsilon), represents the idealized maximum potential delivered by a source, such as a battery. It occurs when there is no current flow in the circuit, serving as a theoretical benchmark for the source’s potential. The measurement of EMF is carried out using a potentiometer, and it is a way of understanding the source’s capability in the absence of external influences.
In real-world scenarios, terminal voltage accounts for internal factors, including the resistance within the source, providing a practical measure of voltage during normal operation. EMF, however, represents an idealized scenario without considering internal factors, serving as a theoretical upper limit. The difference between terminal voltage and EMF is crucial in understanding the behavior and capabilities of electrical sources in both practical and theoretical contexts.
Discover more from PAKTECHPOINT
Subscribe to get the latest posts to your email.