What is Norton’s Theorem? Explanation with Examples

Norton’s Theorem states that any portion of a linear electrical circuit with independent and/or dependent sources and resistances can be replaced by an equivalent circuit consisting of a current source I_sc in parallel with a resistor R_th. Here, I_sc is the short circuit current at the terminals, and R_th is the Thevenin equivalent resistance.

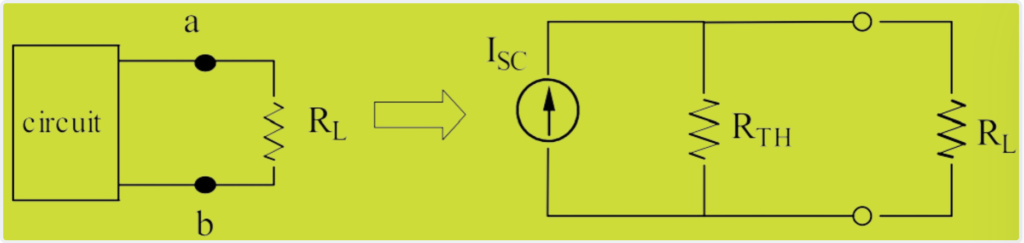
Steps for Applying Norton’s Theorem.

1. Circuit Containing Only Independent Sources:

a. Find the Short Circuit Current I_sc .

1. Short the terminals of interest.
2. Calculate the current through the shorted terminals.

b. Find Thevenin Equivalent Resistance R_th.

1. Deactivate all independent sources (replace voltage sources with short circuits and current sources with open circuits).
2. Calculate the resistance seen from the terminals.

c. Construct Norton’s Equivalent Circuit.

1. Place I_sc in parallel with R_th.
2. Reconnect the load resistor to this equivalent circuit.

2. Circuit Containing Only Dependent Sources:

a. Find the Short Circuit Current I_sc:

1. Short the terminals of interest.
2. Calculate the current through the shorted terminals, considering the dependency relations.

b. Find Thevenin Equivalent Resistance R_th.

1. Apply an external voltage source at the terminals and calculate the resulting current, or apply an external current source and measure the voltage.
2. R_th is the ratio of the applied voltage to the resulting current (or vice versa).

c. Construct Norton’s Equivalent Circuit:

1. Place I_sc in parallel with R_th.
2. Reconnect the load resistor to this equivalent circuit.

3. Circuit Containing Both Independent and Dependent Sources:

a. Find the Short Circuit Current I_sc:

1. Short the terminals of interest.
2. Calculate the current through the shorted terminals, considering both independent and dependent sources.

b. Find Thevenin Equivalent Resistance R_th:

1. Deactivate all independent sources.
2. Use the methods for circuits with dependent sources to determine R_th.

c. Construct Norton’s Equivalent Circuit:

1. Place I_sc in parallel with R_th.
2. Reconnect the load resistor to this equivalent circuit.

Circuit Example of Norton’s Theorem.

By Using Norton’s theorem to find V₀. We use same example as in Thevenin theorem example.

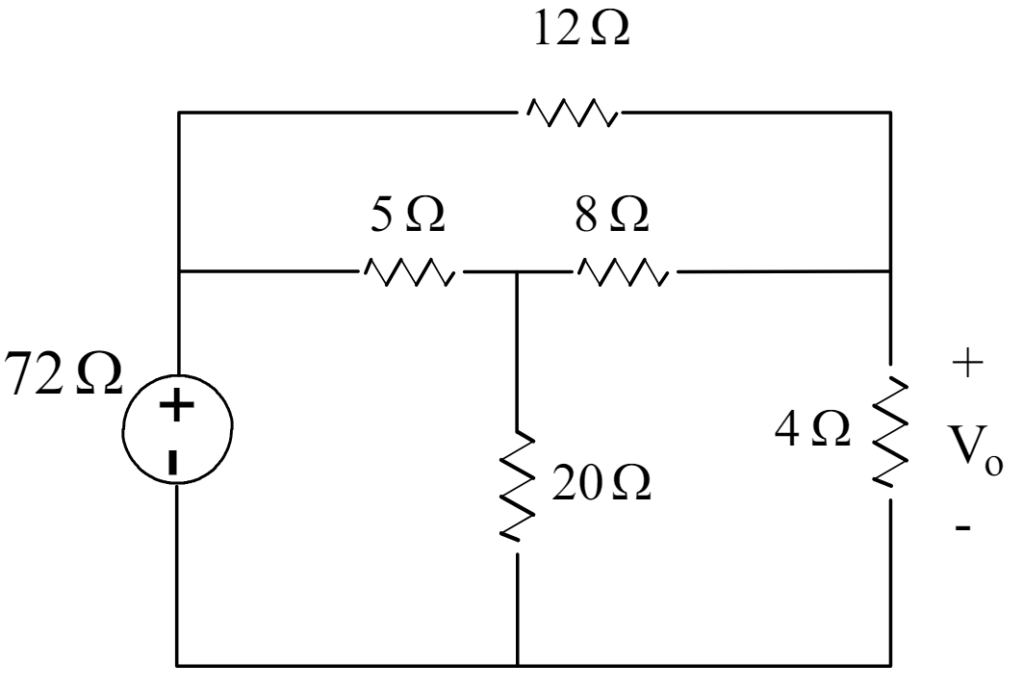
Step 1: Find the Short Circuit Current I_sc .

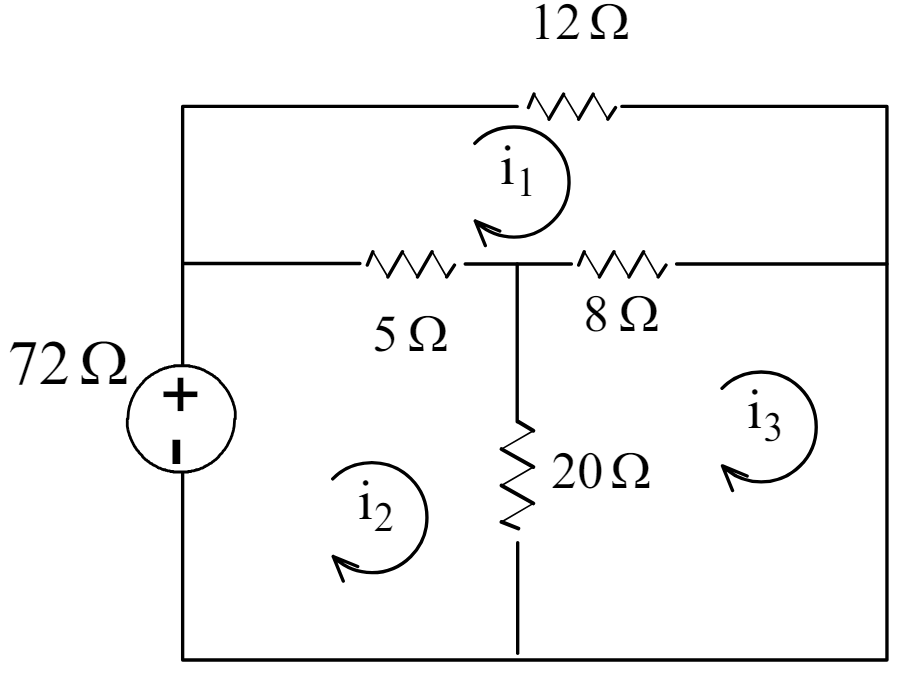
By using KVL around upper loop-1:

12i₁ + 8 (i₁ – i₃ ) + 5 (i₁ – i₂ ) = 0

25 i₁ – 5 i₂ – 8 i₃ = 0 Equation-1

By using KVL around upper loop-2.

5 (i₂ – i₁) + 20 (i₂ – i₃ ) = 72

-5 i₁ + 25 i₂ – 20 i₃ = 72 Equation-2.

By using KVL around lower right loop-3.

8 (i₃ – i₁ ) + 20 (i₃ – i₂) = 0

-8 i₁ – 20 i₂ + 28 i₃ = 0 Equation-3

By solving all these 3 equations by Cramer’s rule.

i₁ = 6 A, i₂ = 12.72 A , i₃ = 10.8 A

So finally we got I_sc = 10.8 A

Step 2: Find Thevenin Equivalent Resistance R_th.

• Deactivate all independent sources.
• Replace Voltage source​ with a short circuit.
• Calculate the resistance seen from the open terminals.

R_th = (12 x 12 ) / (12 + 12) = 144/ 24 = 6Ω

Step 3: Construct Norton’s Equivalent Circuit:

Reconnect the load.

As we know that V₀ = i₂ x R_o

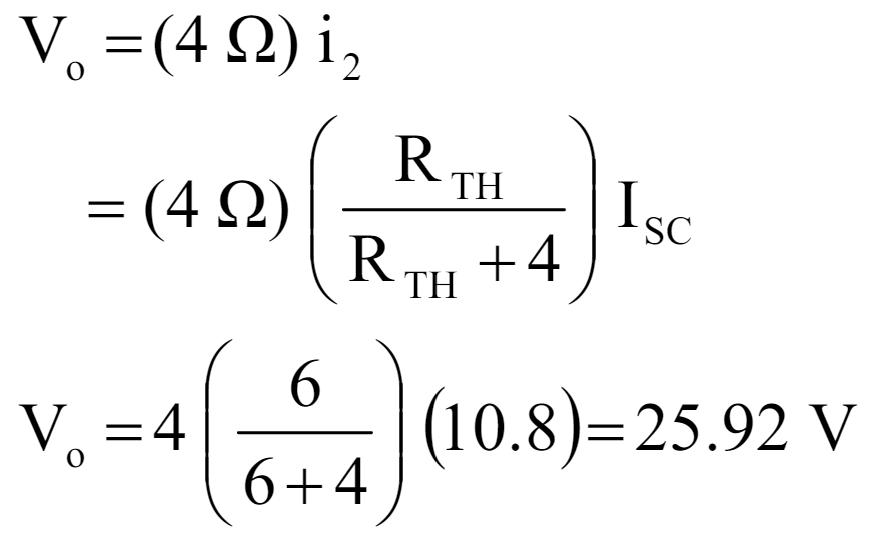
so as shown above calculation V₀ = 25.92 is the same answer as we prove in Thevenin’s Theorem example.