
Thevenin’s Theorem states that any linear, bilateral electrical network with voltage sources and resistances can be replaced by an equivalent circuit consisting of a single voltage source (Vth) in series with a single resistance (Rth) connected to a load.
Thevenin’s Theorem is an analytical method used to simplify complex circuits into a simple equivalent circuit. This equivalent circuit consists of a single voltage source in series with a resistance. By transforming the original complex circuit, Thevenin’s Theorem makes it easier to analyze the behavior of the circuit, especially when different loads are connected to it.
Understanding Thevenin’s Theorem.
Thevenin’s Theorem states that any linear circuit with multiple voltages and resistances can be replaced by an equivalent circuit with a single voltage source (Vth) in series with a single resistance (Rth). This equivalent circuit is connected across the load.
This theorem is particularly useful for simplifying the analysis of power or battery systems and interconnected resistive circuits. It effectively reduces a complex “one-port” network into a simple two-terminal circuit, making calculations more straightforward.
Step-by-Step Procedure of Thevenin’s Theorem.
- Identify the Portion of the Circuit:
- Select the portion of the circuit for which you want to find the Thevenin equivalent. Typically, this involves choosing the two terminals across which you will find the Thevenin equivalent.
- Find the Open Circuit Voltage (VOC or Vth):
- Remove the load resistor (if there is one) across the chosen terminals.
- Calculate the voltage across these open terminals. This voltage is known as the open-circuit voltage (VOC), and it will be your Thevenin voltage (Vth).
- Find the Thevenin Equivalent Resistance (Rth):
- Deactivate all independent sources in the circuit:
- Replace all independent voltage sources with short circuits (i.e., replace each voltage source with a wire).
- Replace all independent current sources with open circuits (i.e., remove the current sources, leaving a break in the circuit).
- Calculate the equivalent resistance seen from the open terminals where the load resistor was connected. This equivalent resistance is the Thevenin resistance (R_th).
- Deactivate all independent sources in the circuit:
- Reconstruct the Thevenin Equivalent Circuit:
- Draw the Thevenin equivalent circuit as a single voltage source (Vth) in series with a single resistance (Rth).
- Reconnect the load resistor to the Thevenin equivalent circuit.
- Analyze the Simplified Circuit:
- Use the Thevenin equivalent circuit to analyze the current through and the voltage across the load resistor.
Thevenin’s Theorem Example.
Find the C Voltage as shown in below circuit by using Thevenin’s Theorem.
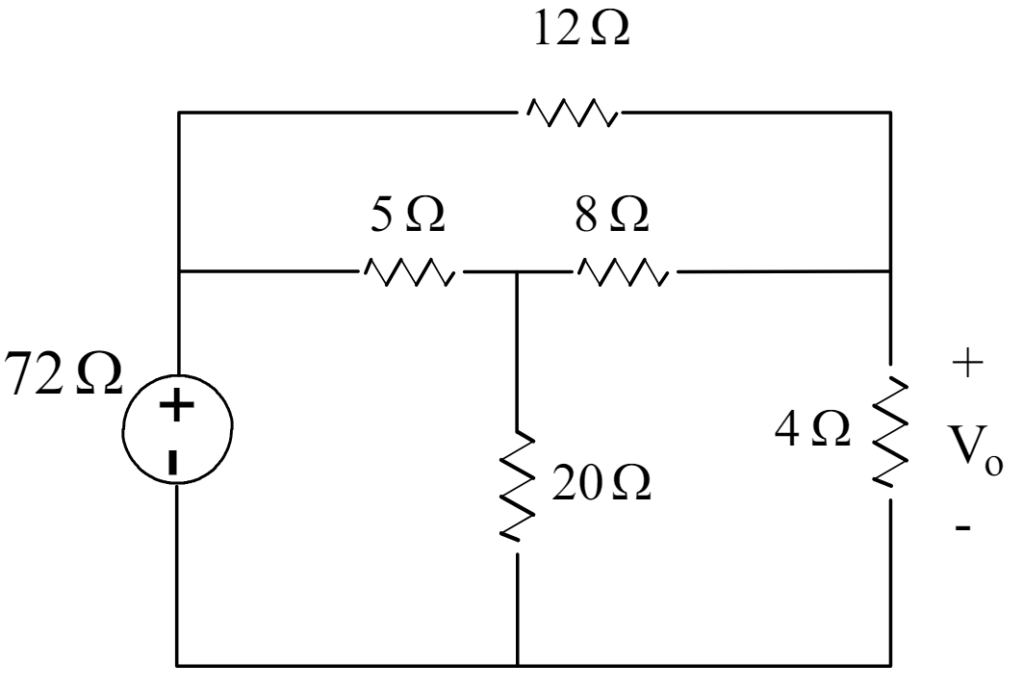
Step 1: Identify the Portion of the Circuit:
Remove the load resistor RL (4Ω).
Step 2: Find the Open Circuit Voltage (VOC or Vth):
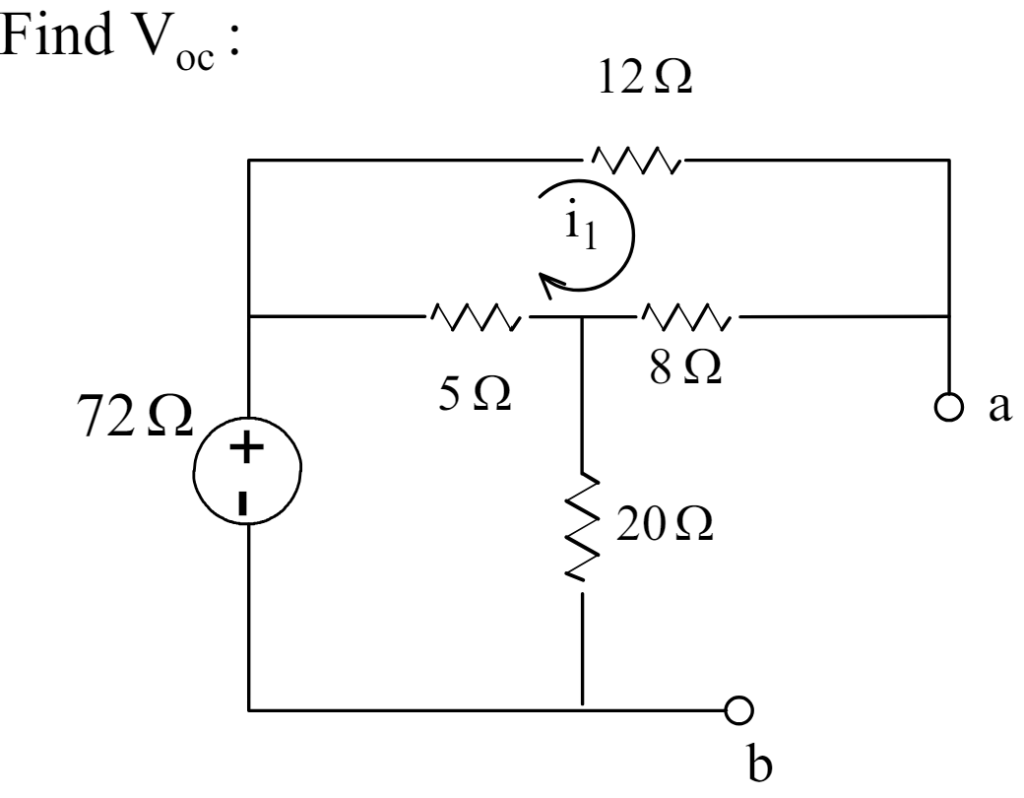
By using KVL for upper loop.
12i1 + 8i1 + 5 (i1 – i2) = 0
25i1 – 5i2 = 0 Equation-1
By applying KVL around lower loop.
5 (i2 – i1) + 20i2 = 72
-5i1 + 25i2 = 72 Equation-2
By solving above 2 equations we got the current values.
i1 = 0.6 A , i2 = 3 A
so finally VOC or Vth will be
VOC = 8i1 + 20 i2 = 64.8 V.
Step 3: Find the Thevenin Equivalent Resistance (Rth):
- Deactivate all independent sources.
- Replace Voltage source with a short circuit.
- Calculate the resistance seen from the open terminals.

Rth = (12 x 12 ) / (12 + 12) = 144/ 24 = 6Ω
Step 4: Reconstruct the Thevenin Equivalent Circuit:
Reconnect the load resistor RL=4Ω to the Thevenin equivalent circuit:
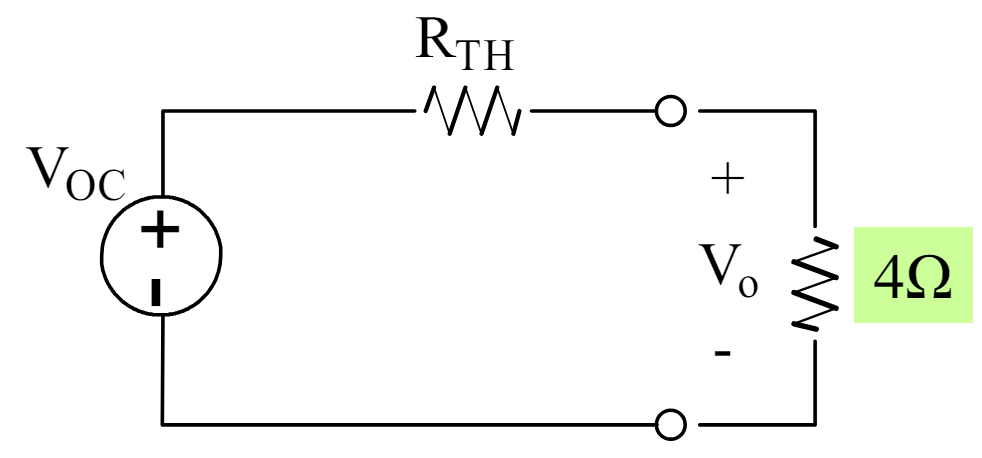
As we know that I = V / R
V = VOC and R = Rth + 4Ω
So, Io = 64.8 / (6 + 4) = 6.48 A
V0 = Io x R = 6.48 x 4 = 25.92 V
Thevenin’s Theorem simplifies the analysis of complex circuits by reducing them to a simple equivalent circuit. This method involves finding the open-circuit voltage, calculating the equivalent resistance with all independent sources deactivated, and reconstructing the circuit with a single voltage source and resistance. This simplification is particularly useful for analyzing circuits with varying loads, making the analysis more manageable and intuitive.